\begin{align}
M_{persp\rightarrow ortho}\begin{pmatrix}
x \ y \ \frac{n+f}{2} \ 1 \
\end{pmatrix}=\begin{pmatrix}
n&0&0&0 \ 0&n&0&0 \ 0&0&n+f&-nf \ 0&0&1&0
\end{pmatrix}
\begin{pmatrix}
x \ y \ \frac{n+f}{2} \ 1 \
\end{pmatrix}=\begin{pmatrix}
nx \ ny \ \frac{n^{2}+f^{2}}{2} \ \frac{n+f}{2}
\end{pmatrix}=\begin{pmatrix}
\frac{2n}{n+f}x \ \frac{2n}{n+f}y \ \frac{n^{2}+f^{2}}{n+f} \ 1
\end{pmatrix}
\end{align}
You can't use 'macro parameter character #' in math mode比较$\frac{n^{2}+f^{2}}{n+f}$与$\frac{n+f}{2}$得 $\frac{n^{2}+f^{2}}{n+f}\geq\frac{n+f}{2}$ 更靠近n面 # Lec5 Rasterazation Triangle - 屏幕是一个数组,数组的单个元素是颜色信息 - Raster\==screen in German - Pixel\==short for "picture for element" ## canonical(规范的) cube to screen - rules 1. 用(x,y)的形式表示 2. x,y为整数 3. 像素表示范围为(0,0)到(width-1,height-1) 4. 中心点在(x+0.5,y+0.5) 5. 因为单个像素占有1\*1空间,所以像素实际占据的屏幕空间为(0,0)~(width,height) ## view port 视口变换 将之前Transformation得到的$[-1,1]\times[-1,1]$的正方形变换到$[0,width]\times[0,height]$上,$z$先不管 viewport transform matrix
You can't use 'macro parameter character #' in math mode这就是双线性插值,从步骤上看, 第一次插值:四个点插值为两个点 第二次插值:两个点插值为一个点 双线性对应的是$2^{2}$的指数$2$ 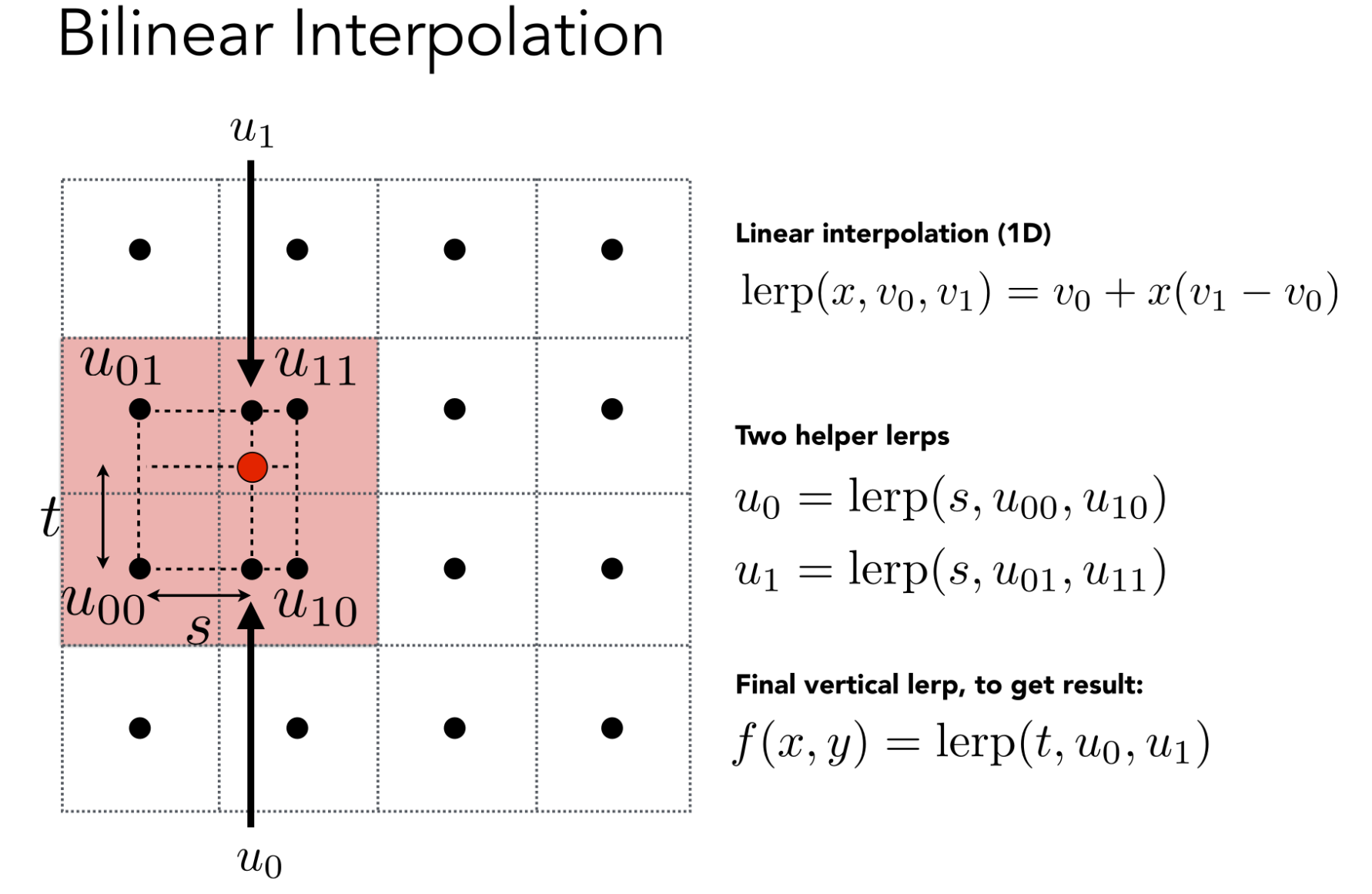 ##### bicubic 性能开销太大,效果最好 ### big case texture太大,而screen太小 一个像素对应的texture范围过大,会造成走样. 从信号的角度看,单个像素对应的texel中,内容变换过快,信号变化频率高,而采样次数太少,从而产生了走样  传统方法处理最右边的情况效果就很差了  处理方式: - super-samping - #### super Sampling 例如单个像素中采样512次,通过提高采样频率避免走样 但是对性能消耗太高 #### range query 既然采样会出现走样的问题,那我就不采样了😡 对于一个像素包含大范围的texture的情况,进行range query 获取某一像素下对应的纹理区域颜色  ##### mipmap ###### what is mipmap Allowing `(fast, approximate, square)` range queries 仅限于正方形,被操作对象为texture “Mip” comes from the Latin “multum in parvo", meaning a multitude in a small space 以原图为$n \times n$为例 在原图的基础上,削减像素数量,为原来的一半,最后图像$level=log_{2}n$.,例如当$n=128$时,最终图为$level 7$ 从性能开销上来看,储存仅仅为原来的$\frac{4}{3}$
You can't use 'macro parameter character #' in math mode 二次度量误差的数据结构采用堆(优先队列),能够迅速查询最小值,也能够快速更新 先对最小值的边进行坍缩,更新堆,再对最小值的边进行坍缩.贪心算法 局部最优!=全局最优,但在绝大部分情况下,这样的贪心算法效果很好  ## shadow mapping 只能处理点光源,只能生成硬阴影(边界没有颜色过度,非常锐利) 点光源没有大小,只是一个点 原图  1. 记录从点光源方向看去的深度图  2. 从相机或人眼看过去的点的深度  3. 比较1,2的深度,来判断是否生成shadow mapping  浮点数本身的比较存在困难.判断浮点数是否相等,被精度问题困扰,比较难. method: - 判断 from eye's 大于 from light's,就生成shadow mapping - 引入bias,若from eye's大于 from light's + bias,就生成shadow mapping #### problem with shadow mapping - Hard shadows (point lights only) - Quality depends on shadow map resolution(general problem with image-based techniques) 不同的分辨率最后的阴影结果不同 - Involves equality comparison of floating point depth values means issues of scale, bias, tolerance # Lec13 ray tracing 1 光线追踪是另一种成像方式. 主要是为了解决rasterization上的 不足: - soft shadow - 光的二次,多次反射 - 间接光照 - glossy reflection - 质量低  - Ray tracing is `accurate`, but is very `slow` - Rasterization: `real-time`(每秒至少30frame), ray tracing: `offline` ## Basic Ray-Tracing Algorithm 三条定义 - 光以直线传播,忽略波动性 - 与其他光线碰撞不会发生交互 - 光线从光源到眼睛(工程上的实现与这个恰好相反,光路可逆性的应用) ### ray casting算法 仅仅考虑了光的一次发射,没有考虑多次反射的光线 4. 从每个像素发出光线 5. 判断物体与光线的交点,与光源的连线是否有遮挡,判断阴影情况  - Pinhole Camera Model 根据与光源的相对情况给进行着色  ### Recursive (Whitted-Style) Ray Tracing 对光线进行多次递归运算,再进行shading. 光线名称做出分类: - primary ray - secondary ray - shadow ray  效果也不错  ### Ray-Surface Intersection (交点) 光线由三个参数来定义. t为时间 o为原点 d为单位方向向量 光线被定义为射线,只有一个方向
r(t)=o+td,0\leq t <\infty
You can't use 'macro parameter character #' in math mode #### Ray Intersection With Sphere 简单的数学运算  #### Ray Intersection With Implicit Surface 计算可以用各种方法实现: - 利用包,数学运算库 - 利用试点,优化法  #### Ray Intersection With Triangle Mesh (最常见的显式表面) 对于给定的mesh与光线,遍历全部三角形求交点.忽略完全平行的请况. 简单但是效率低下  inside与outside判断: 给定一个封闭图形(2D,3D都行),判断一个点是否再图形内部中,从该点射出一条射线, if(交点数量为奇数) 在图形内部 else if(交点数量为偶数) 在图形外部  ##### 平面计算化简法 先算平面与光线的交点,再算交点是否在三角形内  平面的定义: 一个平面法向量$N$与平面上的一个点$P^{\prime}$ 平面是点的集合,根据式子
p:(p-p^{\prime})\cdot{N}=0
You can't use 'macro parameter character #' in math mode来定义平面  对于平面上的这个点,它既在面上,又在射线上 联立方程可解 最后要检查,要求$0 \leq t < \infty$  ##### Möller Trumbore Algorithm 直接求交 用上克拉默法则  #### Accelerating Ray-Surface Intersection 每一个像素发出一条射线,每条射线要与每个objects计算,效果非常差  ##### Bounding Volumes 包围盒 将需要计算交点的物体,用包围盒包起来.包围盒一般都是比较简单的物体.长方形,长方体等等 长方体包围盒由三对相对的面来定义 AABB 包围盒,要求与每个面直角坐标系的某个平面平行,  AABB好处在于,计算时间$t$非常简单  bounding box本身是由几对面求∩表达 光线在bounding box内的时间也是如此 先对各对面,求光线进入时间$t_{min}$,出去时间$t_{max}$. 再求交集,就是对 所有的$t_{min}$求最大值 $max(t_{min})$ 所有的$t_{max}$求最小值 $min(t_{max})$ 暂时不考虑$t_{min}<0$的处理 
You can't use 'macro parameter character #' in math mode iff意为当且仅当   # Lec14 ray tracing 2 Acceleration & Radiometry 传统的ray tracing算法开销太大,要进行加速优化 Using AABBs to accelerate ray tracing ## Uniform grids 在分布均匀的图像中表现较好 不均匀的图像中,表现差 形成规则网格,来加速  对每个小格子进行相交判断. if(与盒子相交) 计算与物体相交情况 else 跳过 通过盒子不一定与物体有交点 不通过盒子与物体一定没有交点  但盒子的分辨率会导致加速效果. 盒子太少,每个盒子都要计算与物体相交情况 盒子太多,要对每个盒子计算是否相交 最好的盒子数量约为 物体数量的27倍  ### Spatial Partitions 空间划分 - oct-tree 八叉树 在d维度下为n叉树,$n=2^{d}$. 该特性导致n叉树实际效果不太好,尤其是在高维的情况下.划分难度高,性能要求高 - kd-tree 总体来说最好的空间划分方式.运用二叉树与AABB的思想.每次划分一刀,每刀方向不同,但与轴align.例如在二维平面中,先横切,再对每个部分竖切. - BSP-tree  #### kd-tree  内部节点与叶子节点的数据结构  类似于二分查找,对每一个叶子节点求是否相交  但kd-tree本身也有一些缺陷 - 某个物体可能被多个AABB划分,导致每个AABB对应的叶子节点中都要储存这个物体的信息 - 给出一个包围盒很难判定它和哪些三角形有交集,也是这个原因最近10年渐渐不用KD树的方法了 为解决,引入Object Partitions 物体划分 Bounding Volume Hierarchy (BVH) ## Object Partitions & Bounding Volume Hierarchy (BVH) 将原有的图形分为好几部分,每一个几何结构只有可能在一个包围盒中出现,即只储存在一个叶子节点中 但也会导致,划分不是严格的划分,bounding box 之间会有相交.质量越好的划分,bounding box 之间的重叠越小   #### 具体划分方法 - Choose a dimension to split 类似kd-tree,横竖横竖地顺序划分 - Heuristic #1: Always choose the longest axis in node 对于长方形的图像,垂直于长,进行划分 - Heuristic #2: Split node at location of median object 尽量从中间的三角形划分,保证划分之后,两个新的叶子节点,所包含的三角形的数量接近,实现平衡二叉树的样子 #### 数据结构  ##### 伪代码 ```c++ Intersect(Ray ray, BVH node) { if (ray misses node.bbox) return; //光线和整个BVH节点不相交,什么也不发生 if (node is a leaf node) //如果光线与BVH的叶子节点相交 test intersection with all objs; //和节点内所有物体都求交 return closest intersection; //返回最近的交点 hit1 = Intersect(ray, node.child1); //如果相交的不是叶子节点,那光线与两个子节点都可能相交 hit2 = Intersect(ray, node.child2); //分别与两个子节点求交 return the closer of hit1, hit2; //返回最近的交点 } ``` ## Basic radiometry (辐射度量学) 鉴于whitted-style模型是一个简化过之后的光线追踪模型,与实际上的情况有着一定的区别. 辐射度量学就是为了做出更加贴近于现实的光线追踪. New terms: Radiant flux, intensity, irradiance, radiance 从物理的角度正确表示光线 ### Radiant flux Radiant Energy为能量,单位为$Q$,焦耳 Radiant flux(power)为单位时间内的能量,$\phi=\frac{dQ}{dt}$,单位为$W$,或者$lm$,流明 其实就是功率  ### Radiant Intensity 光源发出的每单位角的光的功率 $I(\omega)=\frac{d\Phi}{d\omega}\;\;\;\;[\frac{W}{s r}][\frac{l m}{s r}=c d=c a n d e l a]$  what is solid angle? 在二维空间中,用弧长与半径的比值来定义角 在三维空间中,用面积与半径的平方来定义立体角  单位立体角 由高等数学计算得出,球体上单位面积对应的单位立体角为$\mathrm{d}\omega=\frac{\mathrm{d}A}{r^{2}}=\sin\theta\,\mathrm{d}\theta\,\mathrm{d}\phi$  用$\omega$来表示单位向量  对于一个向四面八方发射光线的点光源,光照强度相同,且由积分可算得 $I=\frac{\phi}{4\pi}$ 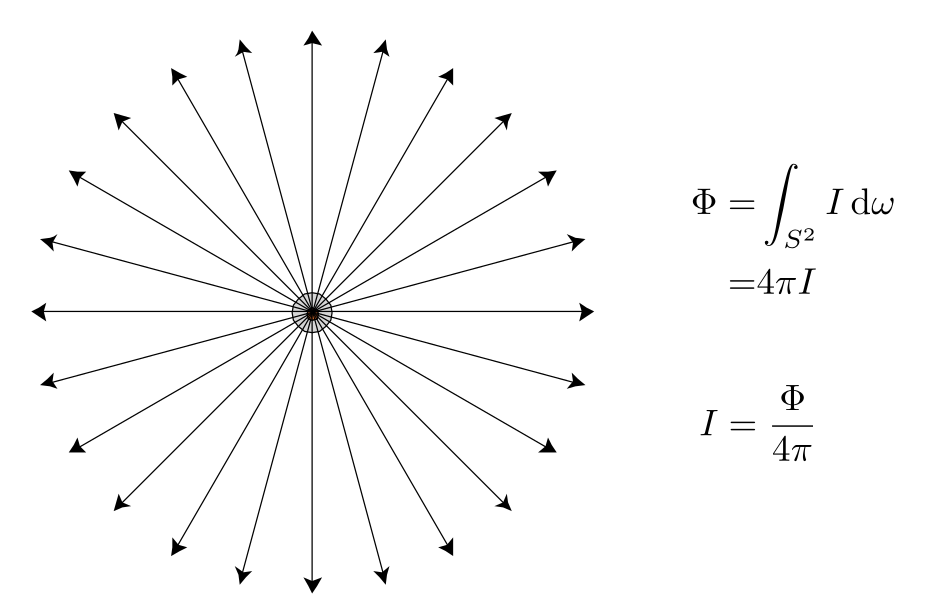 # Lec15 ray tracing 3 ## irradiance 在单位面积上的功率  ## radiance per unit solid angle,per projected unit area 某个面向某个方向辐射能量 要确定面与方向  - Radiance: Irradiance per solid angle - Radiance: Intensity per projected unit area ### Irradiance vs. Radiance 对各个方向的radiance求积分,可以得到irradiance  ## DRBF Bidirectional Reflectance Distribution Function 描述一个unit area 接受的某个方向上的radiance,经过反射后,会向某方向反射的radiance大小.  BRDF 描述每一个入射光与每一个出射光的关系  The Reflection Equation 对于确定的出射方向,计算各个入射方向的积分. 入射的光线除了点光源,还会有一次反射,二次反射等等之后产生的光线. 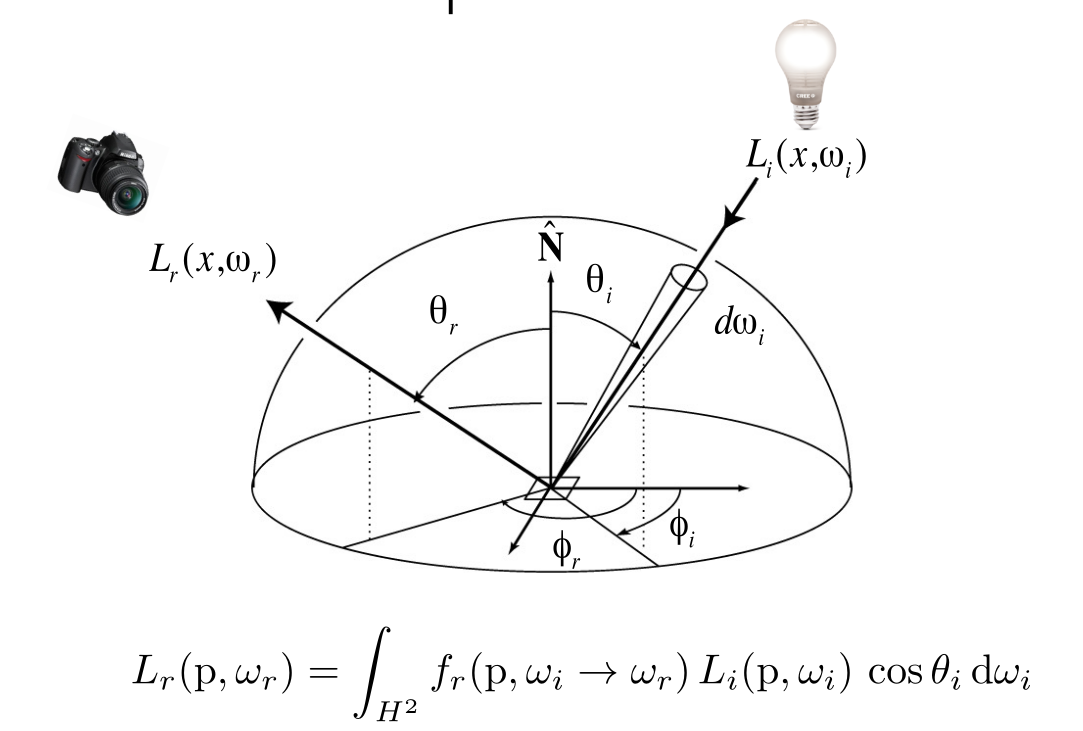 ### rendering equation 除了上方的渲染方程之外,还增加了,观测点本身发光的情况下发出的光源. 求积分,只对上半球体求,下半球体默认为0 $(n \cdot w_{i})$就是$\cos \theta_{i}$  #### 单个点光源  #### 多个点光源 sum函数求和  #### 面光源 integral求积分 面光源是点光源的大集合 对面光源所在的立体角进行积分  #### 其他物体反射光源 光源不一定来自直接光源,也有可能来自其他的物体反射出来的光源 计算物体反射光线对应的立体角  ### 式子化简 对式子进行数学化简 $(x,w_{r})=u$ $(x^{\prime},-w_{i})=v$ 最后化简为只与L,E,K有关的式子 E为自发光,L为光线,K为由BRDF得到的转换矩阵,将入射光线L转换为出射光线 L, E are vectors, K is the light transport matrix    矩阵也有类似于泰勒展开的性质,对于$(I-K)^{-1}$可以展开为$(I+K+K^{2}+K^{3}+...)$,$I$为单位矩阵.  $E$ 为自发光 $KE$ 为直接光照 $K^{2}E$ 为间接光照 全局光照=直接光照+间接光照 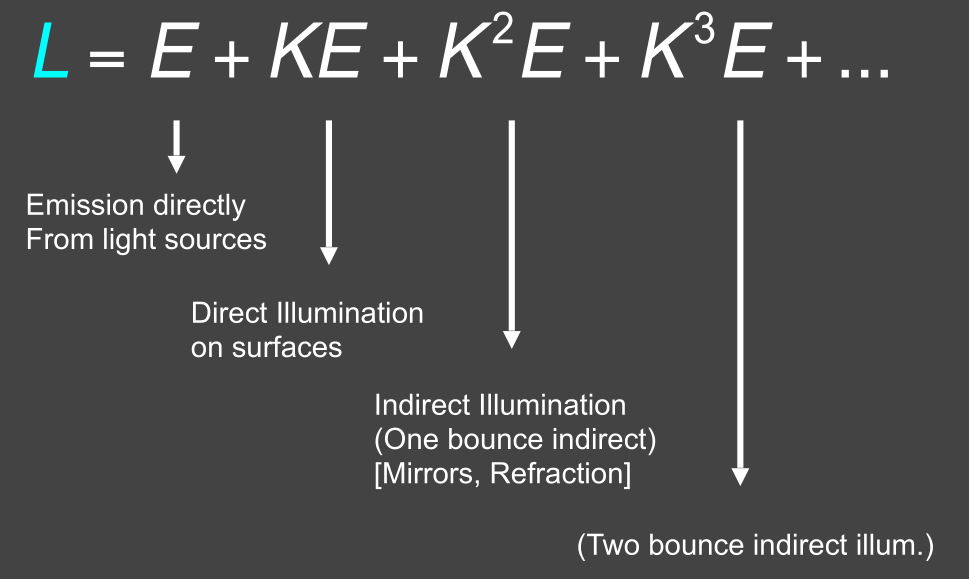 本质就是解方程,计算出变换矩阵$E$和由BFDR定义的$K$就能解出最终$L$的结果 普通的rasterization只对自发光和直接光照处理,虽然也可以处理间接光照,但有难度. ## 概率论复习 # Lec16 ray tracing 4 ## 黎曼积分 对于$f(x)$求积分,黎曼积分方法是,先将积分域内,划分为数量众多的等宽的长方形,对每个长方形求面积,再对面积求sum,最终得到的结果近似积分结果 **微元法** ## Monte Carlo Integration 对于不定积分,最终的计算结果是一个函数$f(x)$ 而对于定积分,最终的计算结果是一个值 传统的方法是,先求积分之后的函数,再带入积分域的上下限,从而求得定积分的值. 但对于某些函数来说,对他求积分函数是相当困难的.既然最终结果为值,那就可以绕过函数求解,直接对结果进行近似. 对于积分域,进行采样操作,对每次采样的结果求面积,再求出定积分.再对多次采样的定积分的值,进行平均. **采样法**  积分通式:  $p(x)$为采样对应的概率密度函数PDF 采样越多,误差越小 在哪个轴上采样,就在哪个轴上积分 ## Whitted-Style Ray Tracing 的问题 Whitted-Style Ray Tracing 模型本身存在局限 对于光线的反射只有两种结果 6. 完全的镜面反射 7. 光线完全漫反射,并不对漫反射的之后的光线进行处理 对于处理glossy材质的反射效果较差.  ## Monte Carlo Solution ### 只考虑直接光照  最简单的对于半球所有方向平均采样的Monte Carlo 积分 $pdf=\frac{1}{2 \pi}$   伪代码: ```c shade(p, wo) Randomly choose N directions wi~pdf Lo = 0.0 For each wi Trace a ray r(p, wi) If ray r hit the light Lo += (1 / N) * L_i * f_r * cosine / pdf(wi) Return Lo ``` ### 分布式光线追踪 处理直接光照+间接光照  伪代码 ```c shade(p, wo) Randomly choose N directions wi~pdf Lo = 0.0 For each wi Trace a ray r(p, wi) If ray r hit the light Lo += (1 / N) * L_i * f_r * cosine / pdf(wi) Else If ray r hit an object at q Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi) Return Lo ``` 进行else判断,对没有找到直接光照的点,寻找间接光照 但这样的算法还是有问题 由于要进行采样,每个角度随机发散出光线,每次间接光照的情况都会导致采样指数增长 $n\neq 1$ 这就叫做分布式光线追踪  ## 路径追踪 仍然是工业界最常用的 处理直接光照+间接光照,但与分布式光线追踪不同 only 1 ray is traced at each shading point ```c shade(p, wo) Randomly choose ONE direction wi~pdf(w) Trace a ray r(p, wi) If ray r hit the light Return L_i * f_r * cosine / pdf(wi) Else If ray r hit an object at q Return shade(q, -wi) * f_r * cosine / pdf(wi) ``` This is path tracing! 但由于光线数量过少,导致结果失真  光线生成 ```c ray_generation(camPos, pixel) Uniformly choose N sample positions within the pixel pixel_radiance = 0.0 For each sample in the pixel Shoot a ray r(camPos, cam_to_sample) If ray r hit the scene at p pixel_radiance += 1 / N * shade(p, sample_to_cam) Return pixel_radiance ``` 路径追踪代码: ```c shade(p, wo) Randomly choose ONE direction wi~pdf(w) Trace a ray r(p, wi) If ray r hit the light Return L_i * f_r * cosine / pdf(wi) Else If ray r hit an object at q Return shade(q, -wi) * f_r * cosine / pdf(wi) ``` 解决了运算指数爆炸的问题,但还存在问题 `The recursive algorithm will never stop!` 但简单地限制光线弹射的次数(即限制递归的次数)是不够令人满意的 这必然会造成某些多次反射的光线没有被计算,被舍弃,能量不守恒了🤔🤔🤔 ### Russian Roulette (RR). 设定一个值P With probability 0 < P < 1, shoot a ray and return the shading result divided by P: `Lo / P` With probability 1 - P, don’t shoot a ray and you’ll get `0` 通过概率判定是否要继续path tracing 期望得到的能量与实际上的能量相等  ```c shade(p, wo) Manually specify a probability P_RR Randomly select ksi in a uniform dist. in [0, 1] If (ksi > P_RR) return 0.0; Randomly choose ONE direction wi~pdf(w) Trace a ray r(p, wi) If ray r hit the light Return L_i * f_r * cosine / pdf(wi) / P_RR Else If ray r hit an object at q Return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR ``` 递归以概率的方式停下来 ### 算法优化 sampling the light 联系之前,信号与采样的关系可以得出 光源越小,光源周围的信号变化越大,对采样要求越高. 这样对投射出去的光线的浪费也越多  但如果能在光源上采样,就不会浪费性能了. 但也带来一个新问题,Monte Carlo methods要求必须,在哪里采样就在哪里积分.对光源面采样,就一定要在光源面上积分,原来对于半球体的积分函数就要转换  两个积分函数之间的积分域相互联系起来.   对于直接光源部分,采用优化算法,不需要RR 对于间接光源部分,采用原来算法  ```c shade(p, wo) # Contribution from the light source. Uniformly sample the light at x’ (pdf_light = 1 / A) L_dir = L_i * f_r * cos θ * cos θ’ / |x’ - p|^2 / pdf_light # Contribution from other reflectors. L_indir = 0.0 Test Russian Roulette with probability P_RR Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi) Trace a ray r(p, wi) If ray r hit a non-emitting object at q L_indir = shade(q, -wi) * f_r * cos θ / pdf_hemi / P_RR Return L_dir + L_indir ``` 最后一个小问题,可能会有物体阻挡在光源与观察点之间 需要增加一个小判断 ```c # Contribution from the light source. L_dir = 0.0 Uniformly sample the light at x’ (pdf_light = 1 / A) Shoot a ray from p to x’ If the ray is not blocked in the middle L_dir = … ``` ## misc   # Lec17 Materials and appearances Material == BRDF ## Diffuse / Lambertian Material 漫反射材质 假设: 没有自发光 每一条入射光的漫反射都是均匀分布 同时入射光本身也均匀分布 那么某着色点的出射光就等于该点所有入射光在小范围内的积分,再乘上BRDF($f_{r}$).  由式子可得, $f=\frac{1}{\pi}$ 设$\rho$为albedo,即颜色反射系数,$\rho \in [0,1]$. 那么完整的$f_{r}=\frac{1}{\pi}$ $\rho$可以是多通道,针对三原色,也可以针对某种原色 ## Glossy material 不完全镜面反射,表面还是存在凹凸  ## Ideal reflective material 即为Perfect Specular Reflection  三维空间中的光线需要两个角度来定义. 侧为$\theta$,俯视为$\phi$ $\theta$平行四边形法 $\phi$俯视角投影 难点在于求这样条件下的BRDF值为多少,感兴趣可以自己推导  ## Specular refraction 折射  右下角的海水也是由光的折射导致的. 由于海水本身的起伏,多道折射光可能射到同一点上,就出现了高光 这种现象叫做caustics,国内翻译作焦散.其实并没有没有散射,翻译不好. 一样也是用$\theta$,$\phi$定义 $n_{i}$,$n_{t}$是折射系数 $\frac{n_{i}}{n_{t}} \gt 1$   仍然存在$\cos \theta_{t}$无意义的情况. 光线在这个折射角无法折射.  人在水下的fov-y仅有$97.2^{\circ}$ ## Fresnel Reflection/Term 不同的入射角,会有不同强度的反射  引出概念Fresnel Term 对于绝缘且$n=1.5$的material来说, 法线夹角与反射率的关系如下,  而对于导体 导体不论任何角度,反射率都极其优秀,镜子都是玻璃再镀银.  S,P极化为光的波动性的体现 一般就取极化平均值 反射率的精准计算:  工程上采用的比较多的是近似方法 Schlick’s approximation 确保 $R_{0}=R_{eff}$ $R_{90}\approx R_{eff}$ ## Microfacet material 神中神,大火都在用的顶级模型.基于物理,模拟光线效果好 Macroscale是从远处看过来的情况,强调是模型材质,忽略细节,视作`平整粗糙`的一整块, Microscale,重视表面的`凹凸细节`,且全部都是`镜面反射`.采用微元法,把每个微元都看作有自己法线的小镜面  由microfacet的原理来定义材质. - glossy是小镜面法线集中 - diffuse是小镜面的法线分散  从数学上计算Microfacet BRDF  $F(i,)h$定义整体折射率 $G(i,o,h)$定义自身阴影遮挡.当光线几乎平行于平面的时候,遮挡产生阴影. $D(h)$定义小镜面总体法线的分布情况,判定漫反射 分母项为推导过程中产生的残留 ## Isotropic / Anisotropic Materials (BRDFs) 各向同性与各向异性材质 - 物理定义 由表面的方向性决定.  - BRDF定义 对入射出射角,转动方位角,如果BRDF不变,为各向共同性 否则为各向异性 各向异性的结果就是一些奇奇怪怪的高光 isotropic只与方位角之差绝对值有关 Anisotropic要求具体的的方位角,即使保持方位角不变的旋转也不行  尼龙是一种接近各向同性的各向异性材质,因为它的表面分布比较有规律  而Velvet天鹅绒的各向同性与各向异性是可以人为改变的. 捋顺冬天的毛毯,就是各向异性 反之就是各向同性  ## Properties of BRDFs - 非负 - 线性  - 可逆性 - 能量守恒  - 对于isotropic材质,可以进行化简,参数可以变为三个.  ## Measuring BRDFs 计算化简之后的BRDF与现实之间还是存在差距.  使用机械测量  鉴于BRDF有$\theta_{i},\theta_{o},\phi_{i},\phi_{o}$四大参数,测量是一个非常复杂繁琐的过程.4D的数据集保存也很困难 测量流程与优化方法:  各种测量方法:  存储要求:  # Lec18 Advanced Topics in Rendering Advanced Light Transport - Unbiased light transport methods - Bidirectional path tracing (BDPT) - Metropolis light transport (MLT) - Biased light transport methods - Photon mapping - Vertex connection and merging (VCM) - Instant radiosity (VPL / many light methods) 有偏与无偏是统计学上的概念  能收敛到的为无偏 不能收敛到的叫有偏 无限采样,无限接近的被叫做一致(consistant) 模糊的就是有偏,无限产生的不模糊就是consistent  从工程的角度看 有偏方法最终的结果可能会与实际差距较大 而无偏方法不管怎么处理,结果都贴近真实 例如下方的Photon mapping 当`n过大`的时候,会产生模糊现象,就是由于Photon Mapping本身是有偏方法,造成`n越大,偏差越大` ## Unbiased light transport ### BDPT 双向的路径追踪  光照能量主要集中在某个漫反射上  对于path tracing非常困难 对于BDPT不错.但BDPT实现难度高,运行速度慢 ### Metropolis Light Transport (MLT) 原理在于,找到一条正确的光路,再在光路周围生成新的推测出来的光路  对于困难的光路比较好用,尤其是specular-diffuse-specular (SDS)这种光路  当然也存在问题咯 无法估计收敛的时间.相较于其他的光线追踪算法,MLT不能较好地估计产生一个比较好的图像所需要的时间 并且由于相邻的像素,在收敛程度上并不存在相关性,导致相邻像素差距较大,噪点过多,图像看着太脏.尤其是在动画方面,前后两帧差距过大,动画不稳定  ## Biased light transport ### Photon Mapping - A biased approach & A two-stage method - Very good at handling Specular-Diffuse-Specular (SDS) paths and generating caustics  原理: 8. 从光源开始发射光线,不管折射与反射,但要在漫反射的位置停下来. 9. 从眼睛(相机)开始,发射sub-path,同样,不管折射与反射,在漫反射位置停下 10. Calculation — local density estimation.求周围$N$个光子对应的面积的密度.$N$人为指定   可以看到,并不是$N$越大,效果越好  这是因为,Photon Mapping 本身是一个有偏的方法. 根本在于,计算密度的时候,我们并不是严格按照定义$\frac{dN}{dA}$,而是计算$\frac{\Delta N}{\Delta A}$(固定数量N对应的面积) 只有当光源,人眼发出的光线越多,$\frac{\Delta N}{\Delta A}$中的$\Delta A$越接近$dA$,效果越好 当接近无限的时候,就能产生consistent的效果 为什么不用固定的$\Delta A$? 很简单,固定的$\Delta A$永远不可能等于$d A$,永远实现不了consistent ### Vertex Connection and Merging A combination of BDPT and Photon Mapping 对于两个sub-path的终点非常接近的情况,会采用Photon Mapping的方法,将终点看作光子,再在两个点存在的面上,计算贡献.从而提高的利用率,减少对于sub-path的浪费 ### Instant Radiosity (IR) 实时辐射度算法 每个光源产生新的光源.实现用直接光的算法,得到间接光的效果  在diffuse中效果好 无法处理glossy 材质 在边缘会有奇怪的发光点  ## Advanced Appearance Modeling - Non-surface models - Participating media - Hair / fur / fiber (BCSDF) - Granular material - Surface models - Translucent material (BSSRDF) - Cloth - Detailed material (non-statistical BRDF) - Procedural appearance ### Non-Surface Models #### Participating media 各种非表面的散射介质(participating medium)fog,could... 在反射中,我们有BRDT描述 在散射中,我们有相位函数(Phase Function)描述  它决定了散射的方向,散射的能量分布,光线传播多远等 rendering方法  需要注意的是,很多看似不是散射介质,而是表面材质的东西,其实也是散射介质. 例如这只巧克力兔子,液体的内部仍然是散射材质,只是不明显,光线很快会在内部消失  #### Hair Appearance ##### Kajiya-Kay Model 将毛发视作一个圆柱 光线在一个圆锥的范围内进行散射,效果一般   ##### Marschner Model T为折射 R为反射 TT即穿过毛发,发生两次折射  cuticle为头发表面,由角质组成 cortex为内部,不同颜色的毛发有不同的,由色素决定的cortex,也能吸收光线  效果非常漂亮  #### Fur Appearance 直接套用人类头发模型效果不够好  原因在于,动物毛发与人类头发本身就存在差异 头发被分为三级,cuticle,cortex,medulla,由于人类的髓质(meddula)本身就比较小,用单个cylinder模型,效果也不错,但是对于动物而言,毛发的髓质层较大,忽略之后,效果差距明显  改用Double Cylinder Model  $TRT^{s}$意为穿透-经过髓质-反射-穿透 其他同理  从之前的三层变为五层结构,增加了$TT^{s}$与$TRT^{s}$层,可以看出它们对于结果的贡献也是极大的  #### Granular Material 颗粒材质  目前处理得还不够好,难度很高 ### Surface Models #### Translucent Material 通透材质 相较于BRDF,增加了表面下的光线散射,叫做BSSRDF. SS应该就是Subsurface Scattering  与BRDF类似,对于面积和角度进行积分.但计算极为困难  因此提出近似方法Dipole Approximation  在表面下生成一个光源,对应的表面上的位置也生成一个光源 可以看到模拟人的皮肤,玉石的效果都很好   #### Cloth 布料模拟 物理上的组成情况 fibers->ply->yarn->cloth  有三种比较主流的渲染方式 - BRDF 简单有效 受材质限制: 对于类似天鹅绒这种本来就不在一个平面上的材质来说,效果差 对针织,在一个平面上的材质,效果好   - Render as Participating Media 当作散射介质进行渲染,与对云烟的渲染类似  - Render as Actual Fibers 最最暴力的算法,直接对每一根纤维进行渲染  ### Detailed appearance 这样子的茶壶虽然效果很好,但不够真实. 原因在于相对于现实世界中缺少的细节:各种划痕   将上面两幅合成之后的效果就好多了  在传统的微表面模型中,$D(h)$是理想化的  法线的高斯分布是极其均匀的.但在正常的情况下,应该是大体符合,部分不同.这就是缺少的细节.  但要对这样充满细节的镜面模型进行渲染开销很大. path sampling经常会出现miss现象  Solution: BRDF over a pixel 对一个规定区域内,求它们的平均法线方向来代替每个微表面的方向  范围越小,细节约多,范围越大,越贴近高斯分布,细节越少  不同范围有不同的P-NDF 不同的材质也有不同的P-NDF  ### Wave Optics 在某些情况下,会有波动光学的特性体现出来   非常困难 ### Procedural Appearance 生成式 表面 利用noise函数生成 生成的结果是三维的内容.相较于表面材质,物体的内部材质也可以通过noise函数查询到.  # Lec19 Cameras, Lenses and Light Fields Imaging = Synthesis + Capture 从成像的角度来看,除了之前的光栅化与光线追踪的虚拟成像之外,还有最最原始的方法,捕捉. 利用小孔成像或者lens+sensor进行成像 ## What’s Happening Inside the Camera? 两大派别: - Pinholes - Lenses Form Image on Sensor ### Pinholes 小孔成像的结果存在问题,所有地方都不会出现应该有的虚化. 因为小孔成像没有焦距的概念,成像缺乏深度信息,自然没有虚化,景深  ### Lenses Form Image on Sensor shutter(快门)控制曝光期间的进光量(irradiance) Sensor Accumulates Irradiance During Exposure 如果缺少lens,单单一个传感器,就会导致记录所有的光线,成像得到的每个pixel都很接近. 因为sensor本身只会记录irradiance,不能区别进光的方向,记录不了radiance.  ### Field of View (FOV) 可以简单计算得FOV与$f,h$的关系 $h$不变,$f$越大,FOV越小 $f$不变,$h$越大,FOV越大  由于历史性的原因,$f$值往往都是参考35mm-format film的标准转换来的   在手机的小底上保持相同的FOV,就需要更小的$f$  ### Exposure Exposure = time \* irradiance time controlled by shutter irradiance controlled by lens aperture(光圈) and focal length 除了光圈大小与快门速度外,还有一个ISO增益. 三者都能影响最后成像的曝光度  - 光圈: $F$越大,光圈越小,挡光越强,越接近于小孔成像,深度信息越少,景深越少 对曝光的影响为指数.$(\frac{F_{1}}{F_{2}})^{2}$ $F2.0$与$F4.0$,前者亮度为后者4倍,越小光圈越大,越亮 - 快门: 快门时间越短,记录的时间信息越少,动作越静止,成像越清晰 对曝光的影响为线性.$1/30$与$1/15$,后者为前者亮度的两倍 标红的几组,在亮度上几乎没有区别,但成像结果也并非是一摸一样 景深与动作模糊存在区别  - ISO: ISO越小,信号放大增益越小,噪点信号与周围信号差距越小,噪点越不明显 乘法计算,且放大效果为线性.12800比100放大128倍 Multiply signal before analog-to-digital conversion Linear effect (ISO 200 needs half the light as ISO 100)  ### shutter side effect - motion blur Doubling shutter time doubles motion blur  - Rolling shutter 快门的开关不是一瞬间发生的,而是一个过程.这就会导致某些地方的光先被sensor接收,某些地方后被接收,成像时间上存在先后顺序 螺旋桨位置就因此发生了扭曲  ### Fast and Slow Photography High-Speed Photography  Long-Exposure Photography  ### Aperture F-N定义为焦距除以直径  ### The Thin Lens Equation/Gaussian Thin Lens Equation 将正常的复杂镜头组视作简单的薄棱镜,来解释各种现象 简单的光学定理,由相似三角形推导得出    ### Defocus Blur 不能正好出现在成像平面上的物体,会产生一个Circle of Confusion (CoC),造成景深模糊的效果.  用相似三角形的原理可以计算得出CoC大小 并且光圈越大,即$F$越小,CoC越明显 $A$为光圈的直径. 将$A=\frac{F}{N}$带入得  ### Depth of Field  景深大小也受到别的参数的影响 what is small enough? 如果成像大小为一个像素或者比一个像素小,就算是锐利的图像.反应到图上就是` Depth of focus`这个范围内成像,都被认为没有CoC  $D_{F}$为最远,$D_{N}$为最近,$D_{S}$为Sensor所在的位置  [在线演示](http://graphics.stanford.edu/courses/cs178/applets/dof.html)中还能看出越$F-N,f$等参数的联系 ## Renderings with Lens Focus 示例  计算过程   # Lec20 Color and Perception Finishing up light field / lumigraph Color • What is color • Color perception • Color reproduction / matching • Color space ## The Plenoptic Function (全光函数) 最完整的全光函数有七大参数 分别表示方向$\theta,\phi$,颜色$\lambda$,时间$t$,位置$V_{x},V_{y},V_{z}$  去掉颜色为黑白 去掉时间为静态照片 去掉位置为固定位置,不能移动 ## 全光函数的光线表示 - 5D,起点与方向五个参数  - 4D,2D点与2D方向  ## Light Field / Lumigraph 光场 一个三维的物体,只要两个参数就能在它的表面贴图中找到对应的位置.再来一个2D的方向,就能确定出一条光线  记录这全部信息,得到的就是光场.在光场中进行简单地查询,就能得到从某个方向看向某点的结果 $2D position+2D direction=2D position+2D position$  进行替换,每个点由两个参数表示.分别为$(u,v)$ $(s,t)$ 并且物体在$(s,t)$的另外一面   固定$(u,v)$,变化$(s,t)$,得到的是相机从$(u,v)$观察物体的结果,与成像相同 但固定$(s,t)$,变化$(u,v)$,得到的结果很奇怪  ## Light Field Camera 苍蝇的复眼就是光场照相机. 在原本成像的位置,加上了透镜,使得已经完成聚焦的光线,被拆分开来,从irridiance变为ridiance,增加了方向性.  光场相机的优点在于,方便后期调节焦距,甚至镜头位置.  原理与苍蝇的复眼相同  如何在后期处理的时候,改变相机位置? 只要某个固定方向的radiance,就可以得到视觉效果.例如图中得到的是从下往上看.  根本的原因在于记录的是光场信息.处理光场信息得到不同的结果 也有一些问题  ## Color ### 光谱  ### SPD Describes distribution of energy by wavelength  太阳与天空的SPD  SPD是线性的,直接相加就行 开两盏灯就是两倍的亮度  ### Biological Basis of Color  有柱形感光细胞,锥形感应颜色细胞.锥形有三种SML  SML对不同的波长感应不同 spectral response curve  每个人的SML也有所不同  最终的结果是对响应曲线的积分,得到SML三个数,再把三个数传递给人脑   ### Metamerism 同⾊异谱 SML三个值影响了最终的颜色.而SML是由积分得到的,也就是说,存在不同的频谱,但是得到的SML值相同. 同⾊异谱的现象存在发生的可能. 一样的太阳不同的频谱  ### Color Reproduction / Matching 我们使用的是加色系统,几种色彩混合的结果趋近于白色. 而现实生活中是减色系统,多种色彩混合的结果趋近于黑色 增色系统由RGB三大参数决定  可能存在RGB某个值是负的情况  匹配函数  对匹配函数进行积分,得到的就是最终的RGB值 例如在500nm波长位置,积分得到的RGB值,就是500nm波长光线的RGB表示的最终结果  ### Color Spaces #### CIE XYZ A Universal Color Space. 是一种人为构造的匹配函数,在科学界使用比较广泛 由$XYZ$三个参数确定,$Y$用来表示亮度  #### HSV Color Space  #### CIELAB Space L*a*b lab系统是由人类的视觉生理特点实验得到  红绿为互补色 蓝黄为互补色 所以才会在ab轴相反方向上采用不同的颜色 ### Gamut (⾊域) Different color spaces represent different ranges of colors So they have different gamuts, i.e. they cover different regions on the chromaticity diagram  不同标准的色域有着不同的色度图覆盖范围 以CIE $XYZ$为例 $xyz$是由$XYZ$归一化之后得到的. 如果把色域放在三维空间中展示,结果不够直观,并且也不好打印到书本上 所以要减少参数. 由于$x+y+z=1$,只需要$xyz$中的两个就够. 因为$Y$用来表达亮度,所以可以固定$Y$的值. 最终只要$XZ$就行.可视化的结果只要$xy$两轴.  白色是最不纯的,越靠近边缘颜色越纯 White at the centroid of the plot (1/3, 1/3) ### Opponent Color Theory There’s a good neurological basis for the color space dimensions in CIE LAB - the brain seems to encode color early on using three axes: - white — black, red — green, yellow — blue - the white — black axis is lightness; the others determine hue and saturation 互补色对于人来说是不能融合的.例如,有黄绿蓝绿深绿,但没有红绿. 还有一个有趣的实验[GAMES101-现代计算机图形学入门-闫令琪 1:24:35](https://www.bilibili.com/video/BV1X7411F744/?p=20&share_source=copy_web&vd_source=2e249bb630e74b68ca9b98c0660aa70b&t=5075) ### color is relative not only color,everything is relative. 就像音乐中,绝对音准虽然很酷,但最重要的还是相对音准. 在颜色中,重要的是相对,而不是绝对的RGB,或者其他颜色空间的参数.    ### Subtractive Color Space 减色系统 CMYK C为蓝绿,M为品红,Y为黄,K为黑  为什么有K呢? 应用中,黑色比较常见,便宜,用CMY来混,成本高 # Lec21 Animation An extension of modeling Represent scene models as a function of time Animation应用视觉残留的原理,短时间输出大量image,得到动画 ## history ## Keyframe Animation  插值法  插值也有Linear interpolation和smooth / controllable interpolation 线性插值效果比较差 ## Physical Simulation 布料模拟,液体模拟    ## Mass Spring System 质点弹簧系统 Example of Modeling a Dynamic System Mass Spring Rope,头发,Mass Spring Mesh模拟    Mass Spring System在布料模拟的效果很好  ### spring 弹簧的情况从最简单理想到最复杂写实