🪴 l4rk's Quartz

13多元函数微分学

13分钟阅读

设函数 在点 的某实心邻域内有定义, 若 在该点的全增量可表示为

{}
{}
{}
{}{}

可微{必}可偏导

可偏导{不一定}可微

Q: 偏导不存在, 可能可微吗?
A: 不可能
可微则偏导必存在 逆否命题为: 偏导不存在一定不可微

Q: 在点 处求 , 它的几何意义是:
A: 保持 y 坐标不变 (y=b), 让 x 坐标在 a 的附近微小地移动, 看函数值 f 的变化率是多少

在 (0, b) 点求

Q: 为什么可偏导不一定可微?
A: 这里的可偏导指的是在 方向上可偏导, 而不是所有方向.
可微⇒所有方向都可偏导
所有方向都可偏导⇒可微
自然仅仅 方向可偏导是推导不出可微的
这是可微要求的

Q: 多元函数 于点 可微的充分条件
A: 若 在点 处的偏导数存在且连续, 则该函数在点 处可微

Q: 多元函数可微的充要条件
A:

Q: 判断函数 在点 处的偏导数是否连续
A: - 使用定义法求点的偏导值

  • 使用公式法求主要区域的偏导值表达式 (主要区域不一定包括点 与分界线)


    计算 与
  • 比较 与 , 与 是否相等
    • 相等: 可能连续, 检查主要区域是否包括了分界线等 coner case
      • 包括了分界线: 连续, 结束
      • 不包括分界线: 可能连续, 使用定义法, 求每条分界线上的偏导.
        分界线为 :
        分界线为 :
    • 不相等: 必然不连续, 结束

Q: 一元函数可微, 可导, 连续, 极限存在相互关系
A: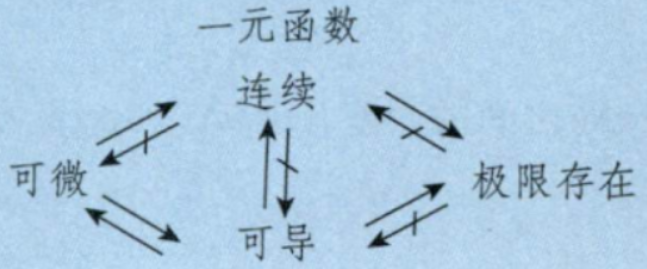

Q: 多元函数一阶偏导连续, 可微, 偏导存在, 连续, 极限存在相互关系
A: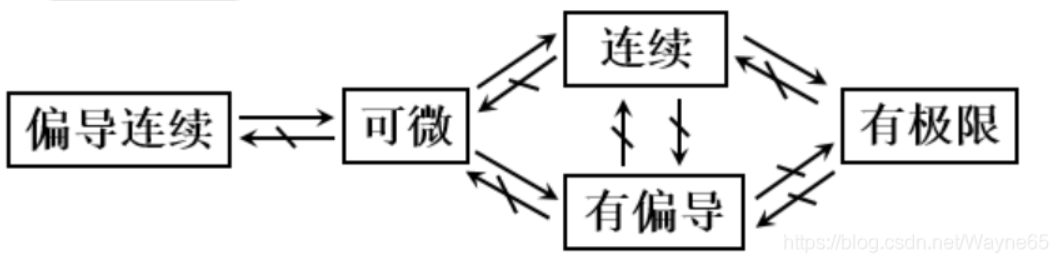

多元函数一阶偏导连续则可微
一阶偏导连续是{充分不必要条件}(充要性判断)

多元函数 于点 一阶偏导连续条件过强
可以减弱为 {一边连续, 一边存在}
一阶偏导于 上连续, 于 上存在
或者
一阶偏导于 上连续, 于 上存在
证明不给出

Q: 多元函数一阶偏导连续则可微
设 于点 处偏导连续, 证明于该点可微
拉格朗日与脱帽法
A:

Q: 可微的判别思路两大判断思路定义法与做商法
A:
做商法
全增量与线性增量做差的结果与 做商, 结果是否是
定义法
判断全增量与线性增量做差, 结果是否是 的高阶无穷小

不论 对哪个变量求导, 也不管求了几次导, 求导后的新函数仍然具有与原函数完全{相同}的{复合结构}

不论 对哪个变量求导, 也不管求了几次导, 保证完全相同的复合结构有什么意义?
不同的偏导, 不同次数的求导, 结果都可以再次进入这个相同的复合结构中, 再次选择某个变量进行求偏导
有助于高次偏导的计算

全微分与全增量区别
全增量{}描述了{实际的函数值变化}
全微分{}提供了{线性近似}

隐函数存在定理
对于由方程 确定的隐函数 , 当 时, 则有
{}

隐函数存在定理的拓展
对于由方程 确定的隐函数 , 当 时, 则有
{}
{}

Q: 二元函数 在点 处取得极值是一元函数 和 分别在 和 处取得极值的什么条件?
A: 充分条件
充分显然成立
在点 处取得极值, 意味着这是邻域一圈中的极值点.
和 只是截取邻域中某个方向. 既然在整个邻域中是极值点, 那么, 在某个方向上自然也是极值点
必要不成立
例如马鞍形状

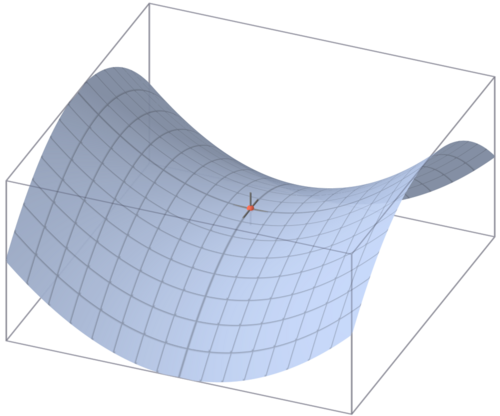
对于两条马鞍线, 在鞍点取到最大值与最小值, 但并不是马鞍面的最值.
必要性显然不成立

二元函数无条件极值, 必要条件
设 在点 处 一阶偏导数存在取极值 则{}
可以推广到三元及三元以上的函数,

Q: 如何理解多元无条件极值的必要条件, 而不是充分条件
A: 设 在点 处 一阶偏导数存在取极值 则
可以推广到三元及三元以上的函数
既然已经在邻域内取到极值, 那么不论哪个方向上,
自然 为必要条件, 而不是充分条件

Q: 二元函数中, 极值点可能出现在哪些位置?
A: 全部偏导数为 的点或者至少有一个一阶偏导数不存在的点

二元函数判断点 取极值的充分条件
判别法
依赖于二次偏导的结果
{c1: }
{c1: }
{c1: }
{c1: }
根据 的不同结果, 极值有不同的情况

  • :{c2: 极值}
  • :{c2: 非极值}
  • :{c2: 判别法失效, 该点可能是极值点, 也可能不是极值点. 利用极值的定义判断或者路径判断}
    当 时, 极值情况判断是极大值还是极小值
    极大值:{c3: }
    极小值:{c3: }
    和二阶导判断凹凸性一样
    不适用于更多元的函数

驻点不一定是极值点
极值点也不一定是驻点

Q: 寻找多元函数极值点的流程
根据必要条件与充分条件寻找
A: - 根据必要条件, 找有可能的点, 即偏导结果为 0 或者偏导不存在的点

  • 根据充分条件, 即 判别法, 求得是极大值还是极小值

Q: 无条件极值中的无条件是什么意思
A: 求解无条件极值时, 只需要考虑函数本身, 不需要考虑任何约束条件 (如等式或不等式约束)

即使中间变量 , 是一个关于 的一个隐函数, 仍然可以用{链式求导规则}求偏导
令 , 求二阶偏导, z 是一个由 确定的隐函数

Q: 用拉格朗日乘数法
求目标函数 在约束条件 下的最值
A: 构造辅助函数
得到方程组, 方程组的个数为未知数加上约束条件的个数





从方程中找出驻点 ,
求得 , 比较后找到最值点

Q: 拉格朗日乘数法找到的最值是最大值还是最小值?
A: 拉格朗日乘数法找到的最值, 是全部的最值.
如果题目要求最大值, 或者最小值, 还要将全部最值的结果比较

当约束条件为{等式}的时候要注意边界的函数值
在使用拉格朗日乘数法解决约束优化问题时, 不仅要考虑通约束范围内, 还需要特别注意边界和端点的函数值. 只有这样, 才能确保找到问题的{全局最优解}.

Q: 为什么有界闭区域上连续函数一定有最值?
A: 极值定理:
一个定义在有界闭区域 上的连续函数, 必定在该区域上取得最大值和最小值

Q: 求有界闭区域 上连续函数 的最值. 有界闭区域 由函数 定义
A: 1. 区域 内部的所有可疑点

  • 驻点:
    解如下方程组, 求出 内部的所有驻点
  • 奇点:
    求出 与 至少一个不存在并且位于 内部的所有奇点
  1. 区域 边界上的所有可疑点 (参数法与拉格朗日乘数法)
  • 参数法: 对约束条件 进行参数化, 将 化为一维函数 , 求 中的极值 (驻点, 无定义点, 端点)
  • 拉格朗日乘数法:
    解如下方程组, 选出可疑点
  • 比较以上所有可疑点的函数值大小, 取其最小者为最小值, 最大者为最大值

与 之间的关系
在一般情况下 =

关系图谱