在 上存在
之间{并没有什么联系, 只是存在罢了}
在 上连续
或者也可以写成
与 之间{充分靠近, 距离是无穷小, 亲密无间}
Q: 可导, 并且 于 点极限存在, 则 在 处连续的证明
A: 证明:
设
只要证明 即可
使用洛必达法则上下为
Q: 在 点极限存在, 在点 的连续性
A: 得不到 是否连续, 可能有 , 条件不够强
Q: 可导, 并且 于 点极限存在, 于点 的连续性
A: 可以得到 连续
在 上可导, 结果存在两种情况
意味着 是 的{高阶}无穷小
意味着 是 的{同阶}无穷小
在 上可导
相较于 在 上连续, , 可知
可导条件{更强}, 不仅仅是 与 之间充分靠近, 亲密无间,
还要求{ 靠近 }的速度比{ 靠近 }的速度{同阶或者更快}
存在, {不一定有}{介值性}
Q: 为什么 存在, 不一定有介值性
A: 介值定理要求 一定有连续性, 存在, 不代表 有连续性
存在, {一定有}{介值性}(达布定理)
具有{介值性}的函数,{不一定}是连续函数
存在, 是连续函数或者有震荡间断点函数 (达布定理)
Q: 存在, 但 为震荡间断点函数
A: 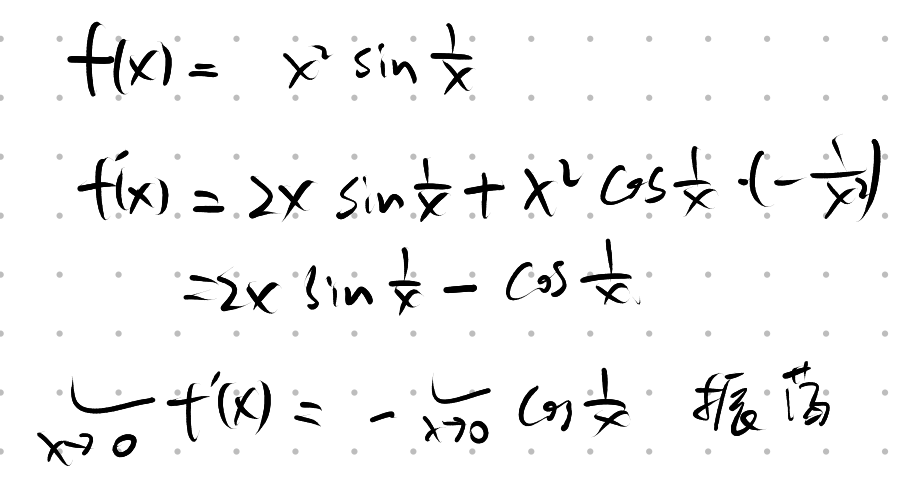
Q: 于区间 上存在, 对于介于 与 之间的任意 , 存在 使得 ,
A: 证明:
假设
设
显然,
一定存在 使得
存在且 , 则 {必}{单调}
Q: 存在且 , 则 必单调, 证明
A: 证明:
假设区间
存在, 一定有介值性,
若 与 异号, 则必有
有条件可知 , 则反证, 与 同号
原函数 具有严格单调
存在, 一定{没有}{第一类间断点}
Q: 存在, 为什么一定没有第一类间断点
A: 存在, 则定义域内处处连续, 具有介值性
既然处处连续就不可能存在跳跃间断点与可去间断点