向量运算
向量内积的定义
设
向量内积的结果是{数}(矩阵? 向量? 数?)
向量正交的定义
若 {向量内积}
显然零向量与任意向量{都}正交 (是否正交)
正交矩阵
正交矩阵的定义
设 A 为
若{
正交矩阵的第一充要条件
{
正交矩阵的第二充要条件
Q: 什么是单位正交? 用
A: 单位:
正交:
什么意思
若
Q: 为什么
A: 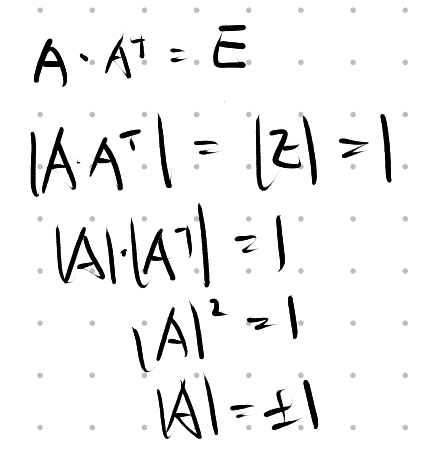
若
则{
若
Schmidt 正交化的定义
设向量组
将其单位化, 得
则
Q: 施密特正交的通用公式
A:
Q: 施密特正交的作用
A: 将一组线性无关的线性向量转化为一组相互正交单位向量
线性相关
线性组合的定义
设向量组为
称{
线性表示的定义
设向量组
{
线性表示的第一充要条件
非零向量
线性表示的第二充要条件
非零向量
零向量可以用{任意的}向量线性表示
Q: 为什么零向量可以用任意的向量线性表示?
A: 从线性表示的定义出发
对于向量组
存在一组数
显然, 存在
使得
向量组等价的定义
设向量组
若向量组可以互相{线性表示}
则向量组等价
Q: 向量组 (I) 与向量组 (II) 等价的充要条件 (代数条件)
A: P 为一个可逆矩阵
则有
即两个向量组可以互相线性表示
Q: 向量组 (I) 与向量组 (II) 等价的充要条件 (秩条件)
A:
Q: 向量组 (I)
为什么向量组等价需要计算
为什么矩阵等价不用计算 r (A, B)
A: 向量组等价与矩阵等价是两个不同的概念
矩阵等价, 意味着可以通过矩阵初等变换, 从矩阵
而向量等价, 意味着向量张成的空间为不仅仅是维度相同, 而且要求张成的空间本身是同一个. 所以需要
线性表示的求法
向量组
对
Q: 行最简形矩阵要求
A: - 主元是
- 主元所在列的其他元素为
- 主元比它上一行的主元靠右 (左/右)
- 所有零行 (如果有) 都在矩阵的底部
线性相关/无关的第一充要条件
向量组
线性相关: 至少有一个向量{可}由其余向量线性表示
线性无关: 任意向量均{不能}由其余向量线性表示
线性相关/无关的第二充要条件
向量组
线性相关: 齐次线性方程组{c1: 除 0 解外还有非零}解
线性无关: 齐次线性方程组{c1: 只有零}解
线性相关/无关的第三充要条件
向量组
线性相关:
线性无关:
线性相关:
线性无关:
Q: 求向量组
A:
线性相关的充分条件
- 含有零向量的向量组线性相关
- 部分相关, 则整体相关
- 高维相关, 则低维相关
- 设向量组
可由向量组 线性表示, 且 ,则 线性相关, 即以少表多 , 则多必相关
逆否命题 : 设向量组线性无关 , 可由向量组 线性表示 , 则 , 即无关被表, 则个数不多.
线性无关的充分条件
- 不含零向量的正交向量组线性无关
- 整体无关, 则部分无关
- 低维无关, 则高维无关
- 不同特征值的特征向量线性无关
Q: 什么是线性无关的低维无关, 则高维无关?
A:
则

判断线性相关/无关的方法
- 定义
- 秩
- V=向量个数
- V<向量个数