秩与解的关系
齐次线性方程组的解与秩的关系
Q: 如何得到一个矩阵
A: 对系数矩阵
每行的第一个非零元素对应的未知数就是主变量其余的未知数被称为自由变量
Q: 矩阵
A: 秩=主变量个数
Q: 如何计算一个矩阵的秩
A: 将矩阵变化为行阶梯形矩阵
得到主变量的个数与自由变量的个数
秩=主变量个数
Q: 非齐次线性方程组的解与秩的关系
A: 
Q: 为什么
从秩的角度证明.
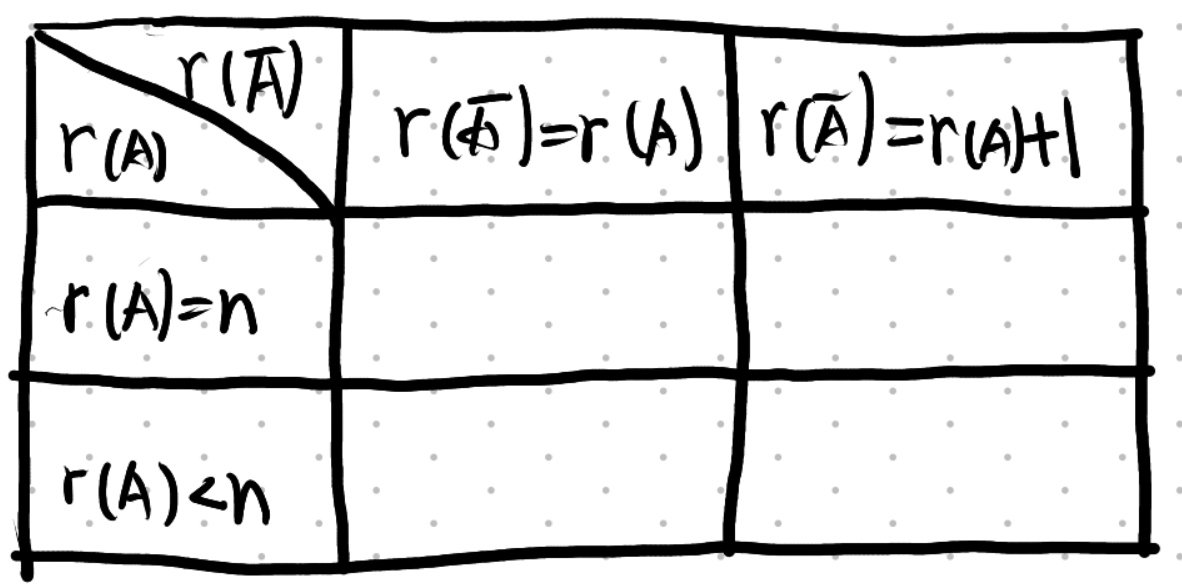
A: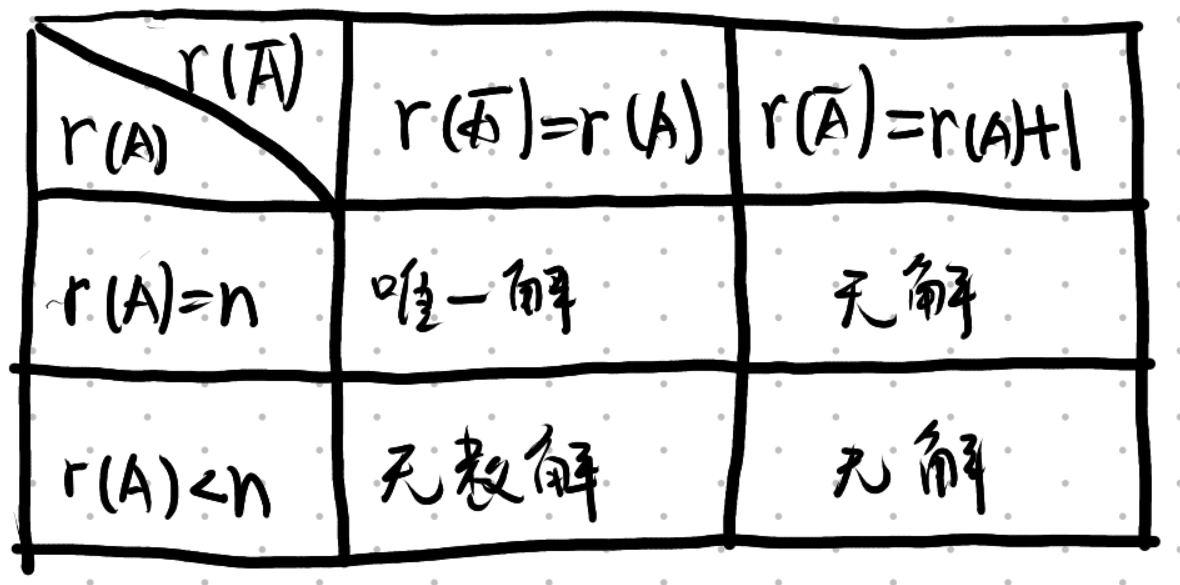
解的性质
齐次加齐次=齐次的解
非齐次减非齐次=齐次的解
齐次加非齐次=非齐次的解
空间与解空间
齐次方程
矩阵张成空间维度为{r (A)}
解空间维度为{n-r (A)}
Q: 基础解系与解空间什么关系?
A: 基础解系是一组描述解空间的基向量
Q: 基础解系中的列向量是否线性相关?
A: 必定线性无关
Q: 同一个解空间中的两个不同基础解系
A:
Q: 基础解系是唯一的吗?
A: 不是
基础解系并不唯一
基础解系是一组描述解空间的基向量
同一个空间可以用多组不同的基向量描述. 基础解系只是其中的一组
Q: 齐次方程
如何求得
A: 将矩阵
自由变量分别取 10000…, 01000…, 00100… 等情况, 解得主变量
组合对应的主变量与自由变量, 得到基础解系
Q: 非齐次方程
有几个线性无关的解?
A:
方程组的通解
A 的基础解系为
则
则
公共解的求解
方程组 1 与方程组 2 的公共解求解
已知方程组 1,2 的具体形式:{联立求解}
已知方程组 1 的具体形式, 方程组 2 的通解:{将方程组 2 的通解代入方程组 1 中, 确定通解的参数, 得到公共解}
已知方程组 1,2 的通解:{令通解相等, 确定参数, 求得公共解}
同解
A 为 m*n 的矩阵, B 为 l*n 矩阵
为{c1:
即{c1: 行}(行 or 列) 向量组等价