15微分方程

Q: 什么是微分方程?
两个条件
A: - 方程

• 含有未知函数的导数 (微分)

Q: 微分方程的阶是?
A: 微分方程中未知函数最高阶导数的阶数

什么是常微分方程?
未知函数为一元函数的微分方程

Q: 阶常系数线性微分方程, 形如?
A: , 其中 都是常数，

Q: 阶齐次线性微分方程与 阶非齐次线性微分方程区别
, 其中 都是自变量 的函数，
A: 右端函数 恒为零, 为 阶齐次线性微分方程
否则称其为 阶非齐次线性微分方程

微分方程的解是{函数}

微分方程解的图形被称为积分曲线

为微分方程 的解
判断是否为通解
若 中含有的{独立常数}的个数等于微分方程的阶数, 则为通解

通解与特解的关系
特解是特殊的通解
确定了通解中的独立常数, 就成为了特解

一阶微分方程

Q: 一阶常微分方程可求解的基本型
A: - 可分离变量
- 直接可分
- 换元可分 ，其中常数 全都不为零. 其解法为令 , 则 , 代人原方程得

• 齐次型微分方程
• 伯努利方程

一阶常微分方程可求解的基本型的特征

• 可分离变量
  • 直接可分 {可以直接分离 }
  • 换元可分 {存在 的形式 }
• 齐次型微分方程 {有关 的函数 }
• 伯努利方程 {存在 的形式伯努利方程一般就考到 的程度, 看到有 的高次就可以尝试使用 }

Q: 一阶微分方程, 直接可分求解
A:

Q: 一阶微分方程, 换元可分求解,
A: 其中常数 全都不为零. 其解法为令 , 则 , 代人原方程得

{非线性}微分方程全部解={通解+特解}
{线性}微分方程全部解={通解}
大纲只要求通解, 不要求全部解

Q: 齐次型微分方程的解法

A: 换元法
令 , 则

于是原方程变为 , 即

形如 的一阶线性微分方程式, 通解为
={}

Q: 一阶线性微分方程式 , 通解
推导
A: 凑出一个求导得到左边的式子

和之前凑被积函数的思路差不多

Q: 一阶线性微分方程通解公式中, 对 的特殊处理
A: 可以不用加上绝对值符号

Q: 为什么, 一阶线性微分方程通解公式中, 对 可以不用加上绝对值符号?
A:

同号得正, 在通解方程中, 符号消去

Q: 伯努利方程形如
A:

Q: 伯努利方程求解

A:
实际上也是个换元法

二阶微分方程

二阶常系数齐次线性微分方程, 用代数表示
{，, 都是常数}

二阶常系数齐次线性微分方程,线性无关解 (基本解组),通解之间的关系
是 的两个线性无关解 (基本解组)
是方程 的通解
通解与线性无关解 (基本解组) 的关系:
{}

Q: 通解的特征方程从何而来?
A: 从 可以看出, 本身与它的一阶导, 二阶导都是常数倍的关系
所以可以用 的形式表示
自然, 就变为了 的形式, 来求解
而这是一个一元二次方程, 自然会有两个解
解的情况根据 判断
对应了三种不同的通解结果

Q: 三种不同特征方程情况对应的三种通解
A:

二阶常系数非齐次线性微分方程, 用代数表示
{，, 都是常数}

二阶常系数非齐次线性微分方程, 解的结构
若 是 的特解
是 的特解, 则
是{}的{特解}

设 都是 的特解, 则 是{}的{某个}解

若 都是 的特解
的某个解={ , }

Q: 若 都是 的特解
的某个解= ,
如何求解 的线性无关解 (基础解系)
A: 在众多的某个解中寻找两个线性无关的解, 组成了齐次方程的基础解系

Q: 二阶常系数非齐次线性微分方程 , 通解求解
A: 1. 使用特征方程求 的通解
2. 根据不同形式的 , 设置带参数的特解 , 代入 , 求解参数, 最终得到特解
3. 为 通解

时, 求特解与通解
设 {}

即 , 求特解
设 {}

Q: 欧拉方程的形式为
A:

Q: 如何求解欧拉方程
A: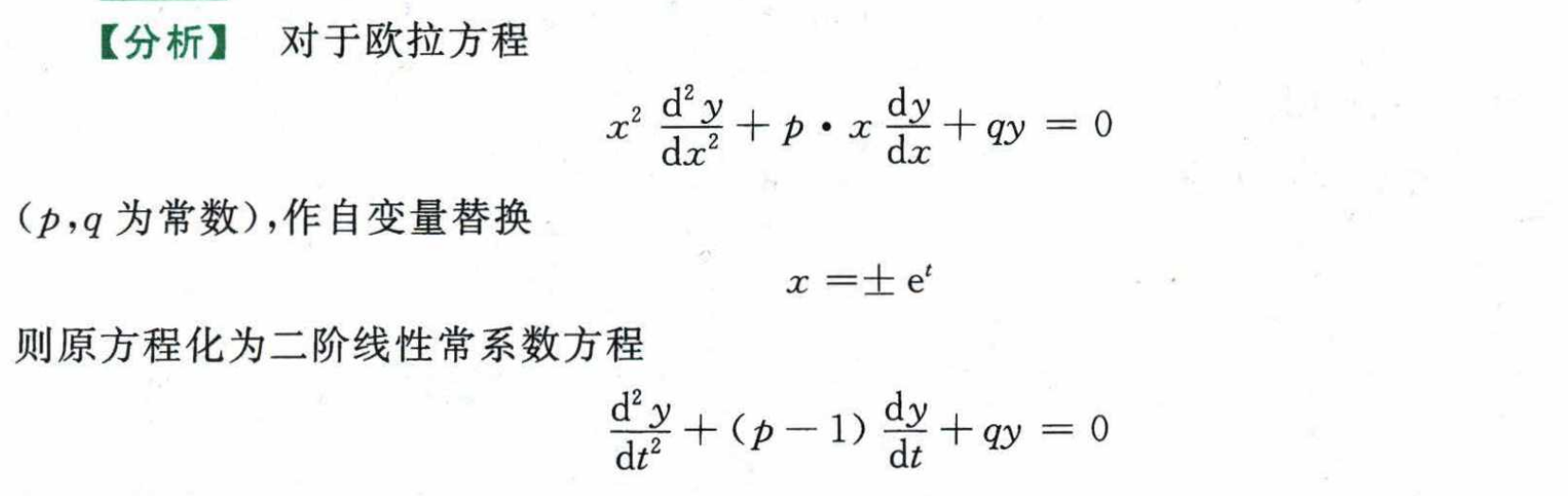

可降阶微分方程

• 赶尽杀绝
  • 特征{不含 }或者{既不含 又不含 }
• 斩草除根
  • 特征{不含 }

Q: 对于一定不含 , 可能不含 的二阶可降微分方程
赶尽杀绝 的解法

A: , 令 ,
原方程变为一阶方程 ,求通解带入即可

Q: 对于不含 的二阶可降微分方程
斩草除根 的解法
, 例如
A: 令 ,
原方程变为
若求得其通解为 , 则由 可得 , 分离变量得
两边积分得 ,即可求得原方程的通解

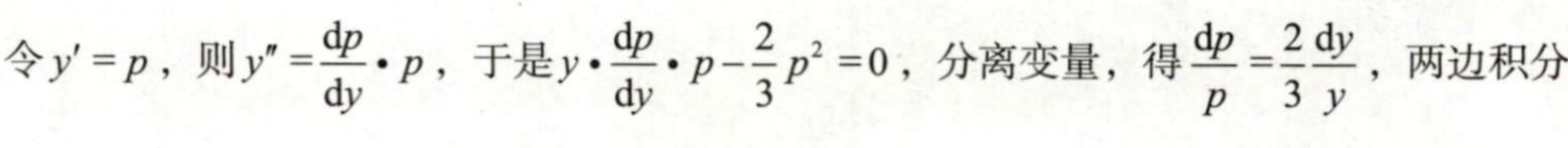
Q: 为什么二阶可降非线性微分方程不用二阶微分线性方程的通解求解?
A: 二阶可降微分方程一般都是非线性的方程
自然不能使用线性方程的解法