Dive into deep learning
Notes
高亮 (link)
terminology
🔤terminology
英 [ˌtɜːmɪˈnɒlədʒi]
美 [ˌtɜːrmɪˈnɑːlədʒi]
n. (某学科的)术语;有特别含义的用语,专门用语;术语学
[ 复数 terminologies ]🔤
高亮 (link)
enumerate
🔤enumerate
英 [ɪˈnjuːməreɪt]
美 [ɪˈnuːməreɪt]
vt. 列举;枚举;计算
[ 第三人称单数 enumerates 现在分词 enumerating 过去式 enumerated 过去分词 enumerated ]🔤
高亮 (link)
Even though we will never see any newlybuilt homes with precisely zero area, we still need the bias because it allows us to express all linear functions of our features (rather than restricting us to lines that pass through the origin).
为什么我们需要bias项
可以表达所有的线性函数,而不是仅仅表达经过原点的函数
高亮 (link)
Even if we believe that the best model for predicting y given x is linear, we would not expect to find a real-world dataset of n examples where y(i) exactly equals w>x(i) + b for all 1 ≤ i ≤ n. For example, whatever instruments we use to observe the features X and labels y, there might be a small amount of measurement error. Thus, even when we are confident that the underlying relationship is linear, we will incorporate a noise term to account for such errors.
为什么即使确定最佳模型是线性的,还是要加上bias
高亮 (link)
While simple problems like linear regression may admit analytic solutions, you should not get used to such good fortune. Although analytic solutions allow for nice mathematical analysis, the requirement of an analytic solution is so restrictive that it would exclude almost all exciting aspects of deep learning.
🔤虽然像线性回归这样的简单问题可能存在解析解,但你也不应指望这样的好运。尽管解析解能够带来优雅的数学分析,但解析解的要求过于严苛,以至于将排除深度学习中几乎所有令人兴奋的方面。🔤
为什么线性回归模型存在解析解,但我们还是不适用?
存在解析解的要求过于严格
高亮 (link)
The key technique for optimizing nearly every deep learning model, and which we will call upon throughout this book, consists of iteratively reducing the error by updating the parameters in the direction that incrementally lowers the loss function. This algorithm is called gradient descent.
梯度下降算法定义
高亮 (link)
One problem arises from the fact that processors are a lot faster multiplying and adding numbers than they are at moving data from main memory to processor cache. It is up to an order of magnitude more efficient to perform a matrix–vector multiplication than a corresponding number of vector–vector operations. This means that it can take a lot longer to process one sample at a time compared to a full batch. A second problem is that some of the layers, such as batch normalization (to be described in Section 8.5), only work well when we have access to more than one observation at a time.
为什么不单次观察,直接更新参数?而选择批处理之后更新参数?
🔤一个问题的产生源于处理器的加法和乘法运算速度远快于将数据从主内存移至处理器缓存的速度。执行矩阵-向量乘法的效率比执行相应数量的向量-向量运算要高出整整一个数量级。这意味着,与处理整批样本相比,逐个处理样本可能要慢得多。第二个问题在于某些网络层(例如将在8.5节介绍的批量归一化层)仅当同时处理多个观测样本时才能有效运作。🔤
图片
minibatch SGD的数学推导
高亮 (link)
In summary, minibatch SGD proceeds as follows: (i) initialize the values of the model
高亮 (link)
parameters, typically at random; (ii) iteratively sample random minibatches from the data, updating the parameters in the direction of the negative gradient.
minibatch SGD的最佳实践
高亮 (link)
After training for some predetermined number of iterations (or until some other stopping criterion is met), we record the estimated model parameters, denoted wˆ , bˆ. Note that even if our function is truly linear and noiseless, these parameters will not be the exact minimizers of the loss, nor even deterministic. Although the algorithm converges slowly towards the minimizers it typically will not find them exactly in a finite number of steps. Moreover, the minibatches B used for updating the parameters are chosen at random. This breaks determinism.
为什么,有限步的迭代,对于即使是没有噪声的精确线性函数,也不能得到精确的解析解?
🔤在训练达到预定的迭代次数(或满足其他停止准则)后,我们记录估计的模型参数,记为ŵ、b̂。需要注意的是,即使函数是严格线性且无噪声的,这些参数也不会是损失的精确最小化点,甚至不具备确定性。尽管算法会缓慢向最小化点收敛,但通常在有限步数内无法精确找到它们。此外,用于更新参数的小批量样本B是随机选取的,这破坏了确定性。🔤
高亮 (link)
orderof-magnitude
数量级
🔤数量级🔤
高亮 (link)
So far we have given a fairly functional motivation of the squared loss objective: the optimal parameters return the conditional expectation E [Y | X] whenever the underlying pattern is truly linear, and the loss assigns large penalties for outliers. We can also provide a more formal motivation for the squared loss objective by making probabilistic assumptions about the distribution of noise.
为什么在linear regression使用squared loss ?
🔤迄今为止,我们已从功能角度对平方损失目标进行了充分论证:当潜在模式真实呈线性时,最优参数返回条件期望E[Y|X],且该损失函数对异常值施以较大的惩罚。此外,通过假设噪声分布的概率模型,我们可为使用平方损失目标提供更形式化的数学推导依据。🔤
图片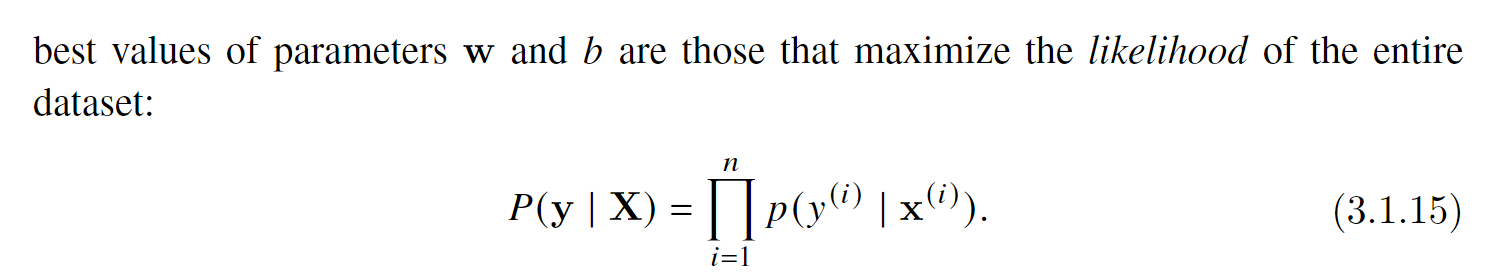
图片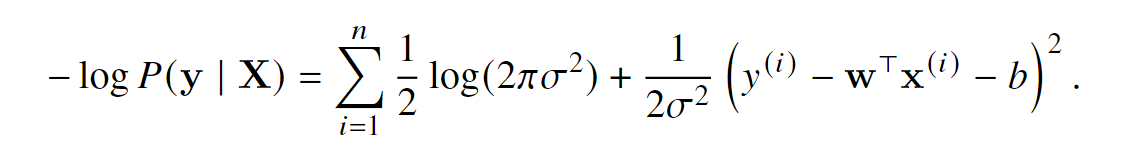
取负数对数似然估计,实现对似然估计乘法计算的简化
高亮 (link)
It follows that minimizing the mean squared error is equivalent to the maximum likelihood estimation of a linear model under the assumption of additive Gaussian noise.
🔤由此可见,在加性高斯噪声假设下,最小化均方误差等价于线性模型的极大似然估计。🔤
为什么?
高亮 (link)
subsume
🔤subsume
英 [səbˈsjuːm]
美 [səbˈsuːm]
vt. 把……归入;把……包括在内
[ 第三人称单数 subsumes 现在分词 subsuming 过去式 subsumed 过去分词 subsumed ]🔤
高亮 (link)
predate
🔤predate
英 [ˌpriːˈdeɪt]
美 [ˌpriːˈdeɪt]
vt. 在日期上早于(先于)
[ 第三人称单数 predates 现在分词 predating 过去式 predated 过去分词 predated ]🔤
高亮 (link)
We invoke Russell and Norvig (2016) who pointed out that although airplanes might have been inspired by birds, ornithology has not been the primary driver of aeronautics innovation for some centuries. Likewise, inspiration in deep learning these days comes in equal or greater measure from mathematics, linguistics, psychology, statistics, computer science, and many other fields.
🔤我们援引Russell和Norvig(2016)的观点指出,尽管飞机的设计可能受到鸟类启发,但数个世纪以来鸟类学并非航空学创新的主要驱动力。同理,如今深度学习的灵感同样甚至更多地源自数学、语言学、心理学、统计学、计算机科学及其他诸多领域。🔤
高亮 (link)
. Assume that we have some data x1, … , xn ∈ R. Our goal is to find a constant b such that Õ i (xi − b)2 is minimized. 1. Find an analytic solution for the optimal value of b. 2. How does this problem and its solution relate to the normal distribution? 3. What if we change the loss from Õ i (xi − b)2 to Õ i |xi − b|? Can you find the optimal solution for b?
- b为 x_d的均值的时候,方差最小
- min sum_i(x_i-b)^2 等价于 正态分布均值 miu 的最大似然估计
高亮 (link)
@add_to_class(A) def do(self): print(‘Class attribute “b” is’, self.b) a.do()
装饰器@add_to_class(A)
即使不在class A 的范围内,也可以向A中添加函数 do()
高亮 (link)
Remove the save_hyperparameters statement in the B class. Can you still print self.a and self.b? Optional: if you have dived into the full implementation of the HyperParameters class, can you explain why?
不行
hyperparameters定义中写明是raise Notimplement,如果在子类中不定义,就会报错
高亮 (link)
X, y = next(iter(data.train_dataloader()))
首次调用 next() 返回第一个批次的数据。后续调用会依次返回后续批次,直到数据耗尽(触发 StopIteration 异常)。
高亮 (link)
What will happen if the number of examples cannot be divided by the batch size. How would you change this behavior by specifying a different argument by using the framework’s API?
When the number of examples in a dataset is not divisible by the batch size in PyTorch, the last batch will contain fewer samples than the specified batch size. For example, with 100 samples and a batch size of 30, the batches will be [30, 30, 30, 10]. This behavior is handled by PyTorch’s DataLoader.
How to Change This Behavior:
To discard the incomplete last batch, set the drop_last=True argument in the DataLoader. This ensures all batches have exactly batch_size samples, and the remaining samples are excluded.
高亮 (link)
In the following we initialize weights by drawing random numbers from a normal distribution with mean 0 and a standard deviation of 0.01. The magic number 0.01 often works well in practice
为什么正态分布的标准差为0.01
高亮 (link)
We should not take the ability to exactly recover the ground truth parameters for granted. In general, for deep models unique solutions for the parameters do not exist, and even for linear models, exactly recovering the parameters is only possible when no feature is linearly dependent on the others. However, in machine learning, we are often less concerned with recovering true underlying parameters, but rather with parameters that lead to highly accurate prediction (Vapnik, 1992)
线性模型参数恢复的条件?
机器学习的目标是,预测准确性还是参数真实性?
高亮 (link)
Fortunately, even on difficult optimization problems, stochastic gradient descent can often find remarkably good solutions, owing partly to the fact that, for deep networks, there exist many configurations of the parameters that lead to highly accurate prediction.
为什么在即使是面对复杂问题,SGD仍然有很好的效果?
高亮 (link)
What would happen if we were to initialize the weights to zero. Would the algorithm still work? What if we initialized the parameters with variance 1000 rather than 0.01?
- still work
- 过大的lr超参数,可能收敛不到loss funcion最小的位置
高亮 (link)
lousy
🔤lousy
英 [ˈlaʊzi]
美 [ˈlaʊzi]
adj. 极坏的,恶劣的;
令人厌恶的,讨厌的;
(让人不快的事物)很多的;
不擅长的;
微薄的,不起眼的;
很难受的,非常不舒服的;
不开心的;
不正确的,不恰当的;满是虱子的;
感到不适的
[ 比较级 lousier 最高级 lousiest ]🔤
高亮 (link)
reinventing the wheel
🔤重复造轮子🔤
这黑话居然是从外国人那里翻译过来的
高亮 (link)
The layer is called fully connected, since each of its inputs is connected to each of its outputs by means of a matrix–vector multiplication.
全连接层的定义
高亮 (link)
nontrivial
高亮 (link)
In PyTorch, the data module provides tools for data processing, the nn module defines a large number of neural network layers and common loss functions. We can initialize the parameters by replacing their values with methods ending with _. Note that we need to specify the input dimensions of the network.
高亮 (link)
How would you need to change the learning rate if you replace the aggregate loss over the minibatch with an average over the loss on the minibatch?
new_lr=lr/minibatch_size
高亮 (link)
aggregate
高亮 (link)
diligently
高亮 (link)
ailments
高亮 (link)
engulf
高亮 (link)
We might cast this problem as just one slice of a far grander question that engulfs all of science: when are we ever justified in making the leap from particular observations to more general statements
高亮 (link)
heuristic
高亮 (link)
IID
independently identical distributions
高亮 (link)
Why should we believe that training data sampled from distribution P(X, Y ) should tell us how to make predictions on test data generated by a different distribution Q(X, Y )? Making such leaps turns out to require strong assumptions about how P and Q are related.
高亮 (link)
population error
高亮 (link)
In classical theory, when we have simple models and abundant data, the training and generalization errors tend to be close. However, when we work with more complex models and/or fewer examples, we expect the training error to go down but the generalization gap to grow.
training set 与 泛化能力的负相关性质
高亮 (link)
falsifiability
高亮 (link)
low training error alone is not enough to certify low generalization error.
高亮 (link)
When we compare the training and validation errors, we want to be mindful of two common situations. First, we want to watch out for cases when our training error and validation error are both substantial but there is a little gap between them. If the model is unable to reduce the training error, that could mean that our model is too simple (i.e., insufficiently expressive) to capture the pattern that we are trying to model. Moreover, since the generalization gap (Remp − R) between our training and generalization errors is small, we have reason to believe that we could get away with a more complex model. This phenomenon is known as underfitting.
underfitting定义
高亮 (link)
Fixing the training dataset, higher-order polynomial functions should always achieve lower (at worst, equal) training error relative to lower-degree polynomials. In fact, whenever each data example has a distinct value of x, a polynomial function with degree equal to the number of data examples can fit the training set perfectly
谁家泰勒展开公式
高亮 (link)
Keeping all else equal, more data almost always leads to better generalization
更多的数据一般来说能够带来更好的泛化能力吗
高亮 (link)
Softmax regression is a single-layer neural network.
高亮 (link)
Assuming a suitable loss function, we could try, directly, to minimize the difference between o and the labels y. While it turns out that treating classification as a vector-valued regression problem works surprisingly well, it is nonetheless unsatisfactory in the following ways: • There is no guarantee that the outputs oi sum up to 1 in the way we expect probabilities to behave. • There is no guarantee that the outputs oi are even nonnegative, even if their outputs sum up to 1, or that they do not exceed 1.
为什么将分类问题视为向量值回归问题会有这些问题?
高亮 (link)
Dating even further back, Boltzmann, the father of modern statistical physics, used this trick to model a distribution over energy states in gas molecules. In particular, he discovered that the prevalence of a state of energy in a thermodynamic ensemble, such as the molecules in a gas, is proportional to exp(−E/kT). Here, E is the energy of a state, T is the temperature, and k is the Boltzmann constant. When statisticians talk about increasing or decreasing the “temperature” of a statistical system, they refer to changing T in order to favor lower or higher energy states. Following Gibbs’ idea, energy equates to error. Energy-based models (Ranzato et al., 2007) use this point of view when describing problems in deep learning.
为什么深度学习中会使用温度控制模型的随机性
高亮 (link)
Note, though, that care must be taken to avoid exponentiating and taking logarithms of large numbers, since this can cause numerical overflow or underflow. Deep learning frameworks take care of this automatically.
自己对每一行进行softmax操作时候,要小心过大的数据.
使用深度学习网络就不用担心,它们会自动处理好