动手学深度学习(PyTorch版)
Notes
高亮 🔗
为了完善业务逻辑,开发人员必须细致地考虑应用程序所有可能遇到的边界情况,并为这些边界情况设计合 适的规则。当买家单击将商品添加到购物车时,应用程序会向购物车数据库表中添加一个条目,将该用户ID与 商品ID关联起来。虽然一次编写出完美应用程序的可能性微乎其微,但在大多数情况下,开发人员可以从上 述的业务逻辑出发,编写出符合业务逻辑的应用程序,并不断测试直到满足用户的需求。根据业务逻辑设计 自动化系统,驱动正常运行的产品和系统,是一个人类认知上的非凡壮举。
完成一个业务逻辑的最佳实践,不断测试优化,包含所有的case corner 直到满足用户需求.
高亮 🔗
现在,假如需要我们编写程序来响应一个“唤醒词”(比如“Alexa”“小爱同学”和“Hey Siri”)。我们试 着用一台计算机和一个代码编辑器编写代码,如 图1.1.1中所示。问题看似很难解决:麦克风每秒钟将收集大 约44000个样本,每个样本都是声波振幅的测量值。而该测量值与唤醒词难以直接关联。那又该如何编写程 序,令其输入麦克风采集到的原始音频片段,输出{是, 否}(表示该片段是否包含唤醒词)的可靠预测呢?我 们对编写这个程序毫无头绪,这就是需要机器学习的原因。
为什么需要机器学习
高亮 🔗
通常,即使我们不知道怎样明确地告诉计算机如何从输入映射到输出,大脑仍然能够自己执行认知功能。换 句话说,即使我们不知道如何编写计算机程序来识别“Alexa”这个词,大脑自己也能够识别它。有了这一能 力,我们就可以收集一个包含大量音频样本的数据集(dataset),并对包含和不包含唤醒词的样本进行标记。 利用机器学习算法,我们不需要设计一个“明确地”识别唤醒词的系统。相反,我们只需要定义一个灵活的 程序算法,其输出由许多参数(parameter)决定,然后使用数据集来确定当下的“最佳参数集”,这些参数 通过某种性能度量方式来达到完成任务的最佳性能。
如何解决抽象的输入与输出映射
高亮 🔗
在机器学习中,学习(learning)是一个训练模型的过程。通过这个过程,我们可以发现正确的参数集, 从而使模型强制执行所需的行为。换句话说,我们用数据训练(train)模型。如 图1.1.2所示,训练过程通常 包含如下步骤: 1. 从一个随机初始化参数的模型开始,这个模型基本没有“智能”; 2. 获取一些数据样本(例如,音频片段以及对应的是或否标签); 3. 调整参数,使模型在这些样本中表现得更好; 4. 重复第(2)步和第(3)步,直到模型在任务中的表现令人满意。
机器学习的一般步骤
图片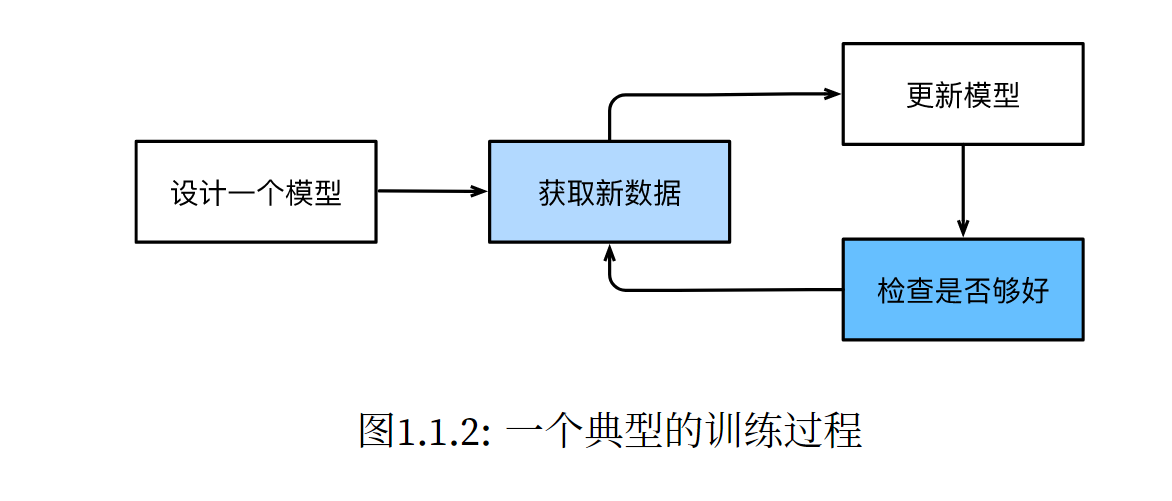
高亮 🔗
当每个样本的特征类别数量都是相同的时候,其特征向量是固定长度的,这个长度被称为数据的维数(dimensionality)。固定长度的特征向量是一个方便的属性,它可以用来量化学习大量样本。
固定特征向量长度的意义,在于方便量化学习大量样本
高亮 🔗
监督学习(supervised learning)擅长在“给定输入特征”的情况下预测标签。每个“特征‐标签”对都称为 一个样本(example)。有时,即使标签是未知的,样本也可以指代输入特征。我们的目标是生成一个模型, 能够将任何输入特征映射到标签(即预测)。
高亮 🔗
总而言之,判断回归问题的一个很好的经 验法则是,任何有关“有多少”的问题很可能就是回归问题。比如: • 这个手术需要多少小时; • 在未来6小时,这个镇会有多少降雨量。 即使你以前从未使用过机器学习,可能在不经意间,已经解决了一些回归问题。例如,你让人修理了排水 管,承包商花了3小时清除污水管道中的污物,然后他寄给你一张350美元的账单。而你的朋友雇了同一个承 包商2小时,他收到了250美元的账单。如果有人请你估算清理污物的费用,你可以假设承包商收取一些基本 费用,然后按小时收费。如果这些假设成立,那么给出这两个数据样本,你就已经可以确定承包商的定价结 构:50美元上门服务费,另外每小时100美元。在不经意间,你就已经理解并应用了线性回归算法。
什么是监督学习中的回归问题
高亮 🔗
虽然回归模型可以很好地解决“有多少”的问题,但是很多问题并非如此。例如,一家银行希望在其移动应 用程序中添加支票扫描功能。具体地说,这款应用程序能够自动理解从图像中看到的文本,并将手写字符映 射到对应的已知字符之上。这种“哪一个”的问题叫做分类(classification)问题。分类问题希望模型能够预 测样本属于哪个类别(category,正式称为类(class))
什么是分类问题
高亮 🔗
回归是训练一个回归函数来输出一个数值;分类是训练一个分类器来 输出预测的类别。
回归与分类的区别
回归是输入特征,输出值
分类是输入特征,输出分类概率
高亮 🔗
分类问题的常见损失函数被称为交叉熵(crossentropy)
分类问题常常使用的损失函数为交叉熵
高亮 🔗
分类可能变得比二项分类、多项分类复杂得多。例如,有一些分类任务的变体可以用于寻找层次结构,层次 结构假定在许多类之间存在某种关系。因此,并不是所有的错误都是均等的。人们宁愿错误地分入一个相关 的类别,也不愿错误地分入一个遥远的类别,这通常被称为层次分类(hierarchical classification)。早期的一 个例子是卡尔·林奈13,他对动物进行了层次分类。 在动物分类的应用中,把一只狮子狗误认为雪纳瑞可能不会太糟糕。但如果模型将狮子狗与恐龙混淆,就滑 稽至极了。层次结构相关性可能取决于模型的使用者计划如何使用模型。例如,响尾蛇和乌梢蛇血缘上可能 很接近,但如果把响尾蛇误认为是乌梢蛇可能会是致命的。因为响尾蛇是有毒的,而乌梢蛇是无毒的。
为什么引入层次结构
高亮 🔗
学习预测不相互排斥的类别的问题称为多标签分类(multi‐label classification)。举个例子,人们在技术博客 上贴的标签,比如“机器学习”“技术”“小工具”“编程语言”“Linux”“云计算”“AWS”。一篇典型的文章可 能会用5~10个标签,因为这些概念是相互关联的。关于“云计算”的帖子可能会提到“AWS”,而关于“机 器学习”的帖子也可能涉及“编程语言”。
什么是多标签分类问题
高亮 🔗
有时,我们不仅仅希望输出一个类别或一个实值。在信息检索领域,我们希望对一组项目进行排序。以网络 搜索为例,目标不是简单的“查询(query)‐网页(page)”分类,而是在海量搜索结果中找到用户最需要的 那部分。搜索结果的排序也十分重要,学习算法需要输出有序的元素子集。换句话说,如果要求我们输出字 母表中的前5个字母,返回“A、B、C、D、E”和“C、A、B、E、D”是不同的。即使结果集是相同的,集内 的顺序有时却很重要。
搜索问题的关键
高亮 🔗
序列学习需要摄取输入序列或预测输出序 列,或两者兼而有之。具体来说,输入和输出都是可变长度的序列,例如机器翻译和从语音中转录文本。
序列学习处理的是变长的输入与输出序列
要求模型具有记忆性并且能够实现不同长短输入与输出之间的映射
高亮 🔗
相反,如果工作没有十分具体的目标,就需要“自发”地去学习了。比如,老板可能会给我们一大堆数据,然 后要求用它做一些数据科学研究,却没有对结果有要求。这类数据中不含有“目标”的机器学习问题通常被 为无监督学习(unsupervised learning)
监督学习的数据中有label,而无监督学习,只有数据
高亮 🔗
生成对抗性网络(generative adversarial networks):为我们提供一种合成数据的方法,甚至像图像和 音频这样复杂的非结构化数据。潜在的统计机制是检查真实和虚假数据是否相同的测试,它是无监督 学习的另一个重要而令人兴奋的领域。
GAN也是一种无监督学习
高亮 🔗
环境是否变化?例如,未来的数据是否总是与过去相似,还是随着时间的推移会发生变化?是自然变化 还是响应我们的自动化工具而发生变化? 当训练和测试数据不同时,最后一个问题提出了分布偏移(distribution shift)的问题。接下来的内容将简要 描述强化学习问题,这是一类明确考虑与环境交互的问题。
强化学习的提出
图片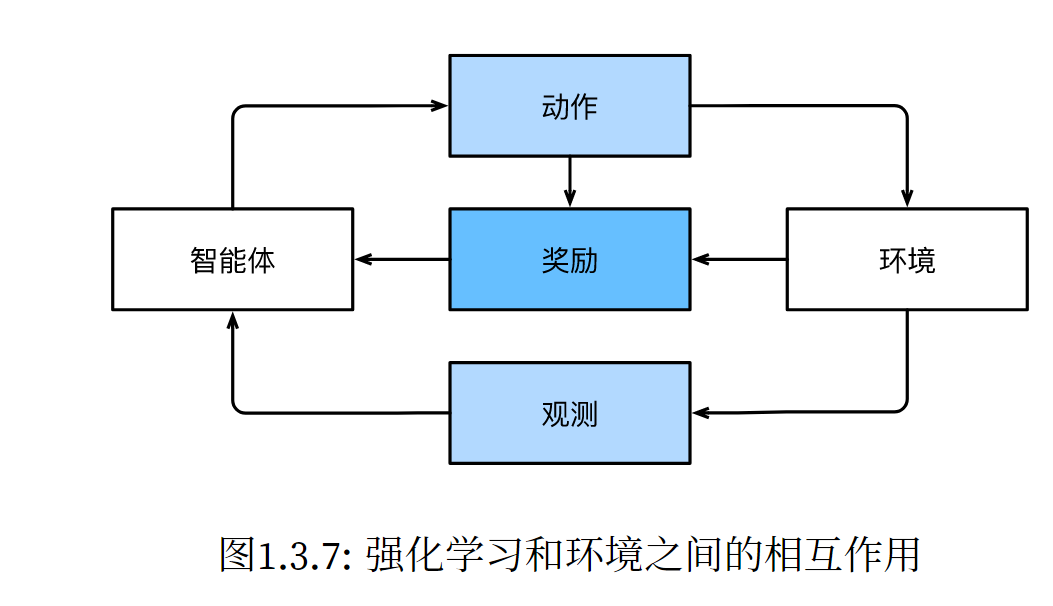
强化学习使用奖励机制,实现与环境的交互
高亮 🔗
当环境可被完全观察到时,强化学习问题被称为马尔可夫决策过程(markov decision process)。当状态不 依赖于之前的操作时,我们称该问题为上下文赌博机(contextual bandit problem)。当没有状态,只有一组 最初未知回报的可用动作时,这个问题就是经典的多臂赌博机(multi‐armed bandit problem)。
强化学习的分类
高亮 🔗
通过平均16名成年男性的脚的长度,可以得出一英尺的长度。
高亮 🔗
神经网络(neural networks)的得名源于生物灵感。一个多世纪以来(追溯到1873年亚历山大·贝恩和1890年 詹姆斯·谢林顿的模型),研究人员一直试图组装类似于相互作用的神经元网络的计算电路。随着时间的推移, 对生物学的解释变得不再肤浅,但这个名字仍然存在。其核心是当今大多数网络中都可以找到的几个关键原 则: • 线性和非线性处理单元的交替,通常称为层(layers); • 使用链式规则(也称为反向传播(backpropagation))一次性调整网络中的全部参数。
神经网络的关键原则
高亮 🔗
经过最初的快速发展,神经网络的研究从1995年左右开始停滞不前,直到2005年才稍有起色。这主要是因为 两个原因。首先,训练网络(在计算上)非常昂贵。在上个世纪末,随机存取存储器(RAM)非常强大,而计 算能力却很弱。其次,数据集相对较小。事实上,费舍尔1932年的鸢尾花卉数据集是测试算法有效性的流行 工具,而MNIST数据集的60000个手写数字的数据集被认为是巨大的。考虑到数据和计算的稀缺性,核方法 (kernel method)、决策树(decision tree)和图模型(graph models)等强大的统计工具(在经验上)证明 是更为优越的。与神经网络不同的是,这些算法不需要数周的训练,而且有很强的理论依据,可以提供可预 测的结果。
为什么1995年之后神经网络的研究停滞不前
高亮 🔗
大约2010年开始,那些在计算上看起来不可行的神经网络算法变得热门起来,实际上是以下两点导致的:其 一,随着互联网的公司的出现,为数亿在线用户提供服务,大规模数据集变得触手可及;另外,廉价又高质 量的传感器、廉价的数据存储(克莱德定律)以及廉价计算(摩尔定律)的普及,特别是GPU的普及,使大 规模算力唾手可得。
深度学习得以发展的根本原因
图片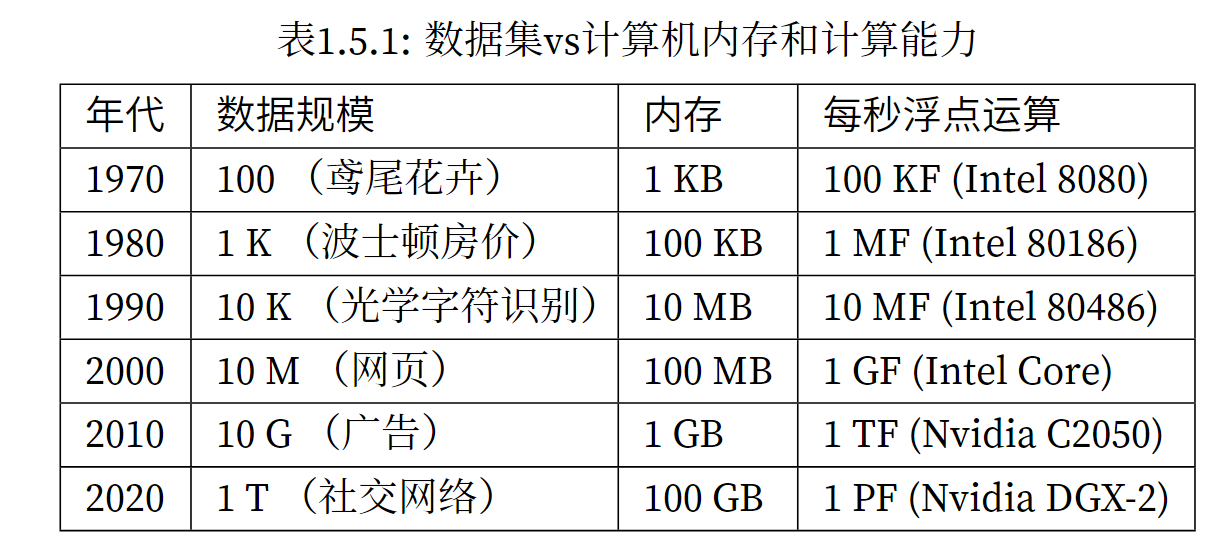
高亮 🔗
除了端到端的训练,人们正在经历从参数统计描述到完全非参数模型的转变。当数据稀缺时,人们需要依靠 简化对现实的假设来获得有用的模型。当数据丰富时,可以用更准确地拟合实际情况的非参数模型来代替。 在某种程度上,这反映了物理学在上个世纪中叶随着计算机的出现所经历的进步。现在人们可以借助于相关 偏微分方程的数值模拟,而不是用手来求解电子行为的参数近似。这导致了更精确的模型,尽管常常以牺牲 可解释性为代价。
从参数统计描述到完全非参数模型的转变,有什么代价
高亮 🔗
对于任意具有相同形状的张量,常见的标准算术运算符(+、-、*、/和**)都可以被升级为按元素运算。我 们可以在同一形状的任意两个张量上调用按元素操作。
相同形状的张量上,可以直接对元素进行标准算数运算
高亮 🔗
在上面的部分中,我们看到了如何在相同形状的两个张量上执行按元素操作。在某些情况下,即使形状不同, 我们仍然可以通过调用 广播机制(broadcasting mechanism)来执行按元素操作。这种机制的工作方式如 下: 1. 通过适当复制元素来扩展一个或两个数组,以便在转换之后,两个张量具有相同的形状; 2. 对生成的数组执行按元素操作。
广播机制的两大工作方式
图片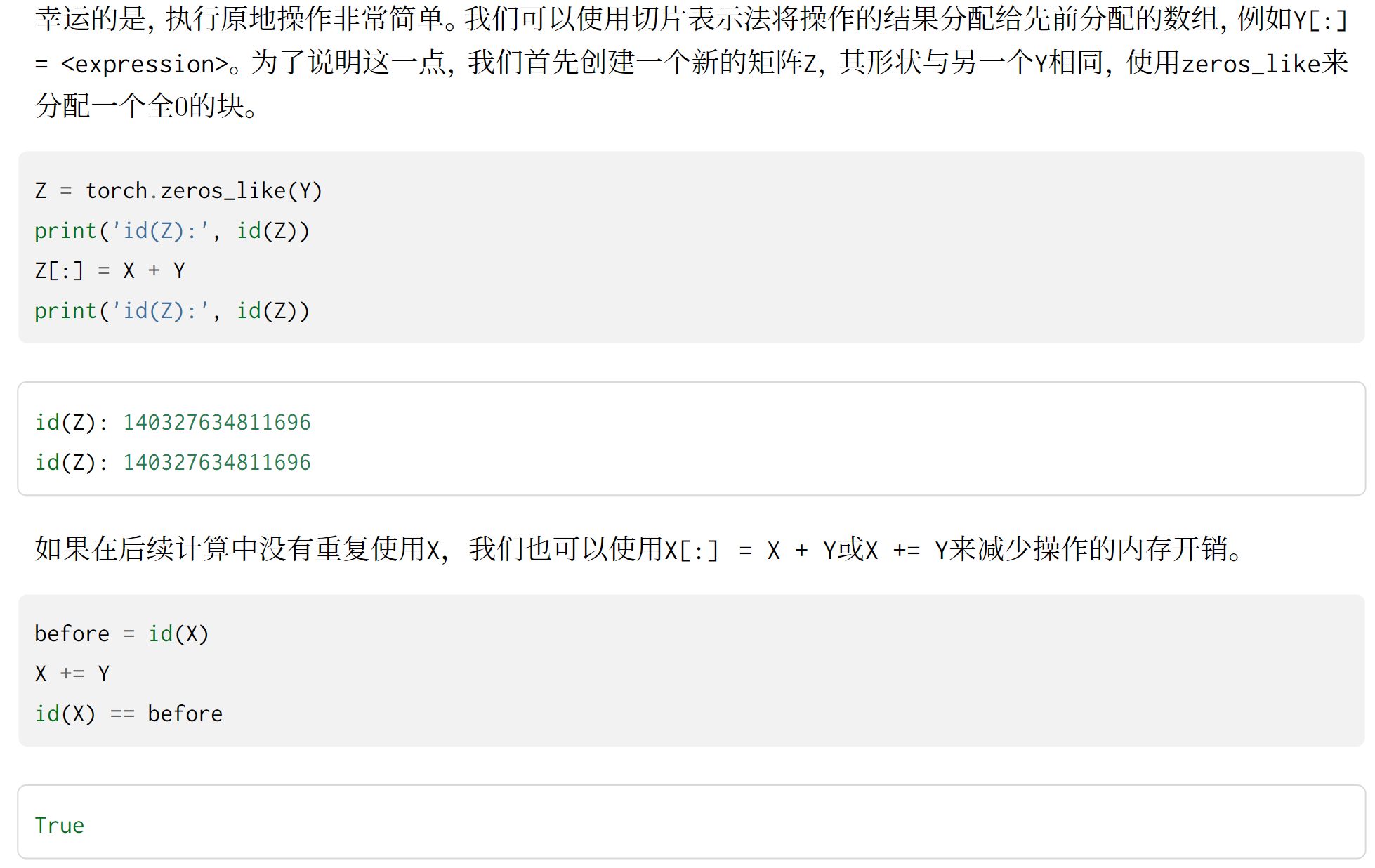
如何使用切片或者+=方法减少内存开销
高亮 🔗
大量文献认为列向量是向量的默认方向,在本书中也是如此。
列向量被设置为向量的默认方向
高亮 🔗
在数学表示法中,如果我们想 说一个向量x由n个实值标量组成,可以将其表示为x ∈ Rn。向量的长度通常称为向量的维度(dimension)。
高亮 🔗
请注意,维度(dimension)这个词在不同上下文时往往会有不同的含义,这经常会使人感到困惑。为了清楚 起见,我们在此明确一下:向量或轴的维度被用来表示向量或轴的长度,即向量或轴的元素数量。然而,张 量的维度用来表示张量具有的轴数。在这个意义上,张量的某个轴的维数就是这个轴的长度。
维度对于向量/轴与张量的不同意义
高亮 🔗
尽管单个向量的默认方向是列向量,但在表示表格数据集的矩阵中,将每个数据样本作为矩 阵中的行向量更为常见。
单个向量与矩阵的方向不同
单个向量的默认方向为列向量
矩阵中向量的默认方向为行向量
高亮 🔗
默认情况下,调用求和函数会沿所有的轴降低张量的维度,使它变为一个标量。我们还可以指定张量沿哪一 个轴来通过求和降低维度。以矩阵为例,为了通过求和所有行的元素来降维(轴0),可以在调用函数时指 定axis=0。
对矩阵的行(axis=0)进行求和,实现降维
高亮 🔗
sum_A = A.sum(axis=1, keepdims=True)
如何保持dim不变
高亮 🔗
矩阵‐矩阵乘法可以简单地称为矩阵乘法,不应与“Hadamard积”混淆。
矩阵乘法要求第一个矩阵的列数等于第二个矩阵的行数,而Hadamard积要求两个矩阵的维度完全相同
高亮 🔗
第一个 性质是:如果我们按常数因子α缩放向量的所有元素,其范数也会按相同常数因子的绝对值缩放: f (αx) = |α|f (x).
范数的绝对齐次性
高亮 🔗
三角不等式: f (x + y) ≤ f (x) + f (y).
范数的三角不等式
高亮 🔗
范数必须是非负的: f (x) ≥ 0.
范数的非负性
图片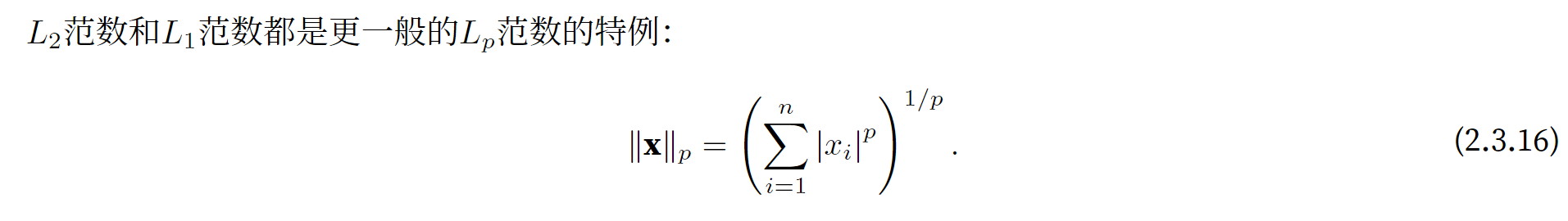
范数的本质是一个 将向量映射到标量的函数
高亮 🔗
Frobenius范 数 满 足 向 量 范 数 的 所 有 性 质, 它 就 像 是 矩 阵 形 向 量 的L2 范 数。
高亮 🔗
运行A/A.sum(axis=1),看看会发生什么。请分析一下原因?
>>>a/a.sum(axis=1)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: operands could not be broadcast together with shapes (2,3,4) (2,4)
形状不匹配
高亮 🔗
考虑一个具有形状(2, 3, 4)的张量,在轴0、1、2上的求和输出是什么形状?
axis=0:(3,4)
axis=1:(2,4)
axis=2:(2,3)
高亮 🔗
因此,我们可以将拟合模型的任务分解为两个关键问题: • 优化(optimization):用模型拟合观测数据的过程;
高亮 🔗
• 泛化(generalization):数学原理和实践者的智慧,能够指导我们生成出有效性超出用于训练的数据集 本身的模型
高亮 🔗
我们可以连结一个多元函数对其所有变量的偏导数,以得到该函数的梯度(gradient)向量。具体而言,设 函数f : Rn → R的输入是一个n维向量x = [x1, x2, … , xn]⊤,并且输出是一个标量。函数f (x)相对于x的梯度 是一个包含n个偏导数的向量: ∇xf (x) = [ ∂f (x) ∂x1 , ∂f (x) ∂x2 , … , ∂f (x) ∂xn ]⊤ ,
高亮 🔗
一个标量函数关于向量x的梯度是向量,并且与x具有相同的形状
标量函数: 结果为一个标量的函数
对于标量函数f(x),不管x是向量还是一个标量,x.grad与x 的形状是相同的
高亮 🔗
torch.dot(x, x)
X^t * X 转秩乘法
高亮 🔗
对非标量调用backward需要传入一个gradient参数,该参数指定微分函数关于self的梯度。
非标量调用backward的特殊要求
高亮 🔗
y=x*x u = y.detach()
用detach()函数进行截断
z=u*x
计算z关于x 的反向 传播的时候,u被当作一个与x 无关的变量
高亮 🔗
使用自动微分的一个好处是:即使构建函数的计算图需要通过Python控制流(例如,条件、循环或任意函数 调用),我们仍然可以计算得到的变量的梯度。在下面的代码中,while循环的迭代次数和if语句的结果都取 决于输入a的值。
即使是控制流,也可以得到正确的梯度
高亮 🔗
为什么计算二阶导数比一阶导数的开销要更大?
二阶导需要经过两次导数
高亮 🔗
在运行反向传播函数之后,立即再次运行它,看看会发生什么。
没有运行grad.zero_(),使得,运行一次,grad累加一次
高亮 🔗
fair_probs = torch.ones([6]) / 6
六个位置中,有一个为1,其他为0
高亮 🔗
以上也是概率论的公理,由科尔莫戈罗夫于1933年提出。有了这个公理系统,我们可以避免任何关于随机性 的哲学争论;相反,我们可以用数学语言严格地推理。
数学杀死了哲学
高亮 🔗
在 2.6.2节中,第一个测试更准确。为什么不运行第一个测试两次,而是同时运行第一个和第二个测试?
一个测试出现假阳性的可能,远远大于两个测试同时出现假阳性的可能
高亮 🔗
print(dir(torch.distributions))
查询随机数生成模块中的所有属 性
高亮 🔗
help(torch.ones)
有关如何使用给定函数或类的更具体说明
高亮 🔗
仿射变换的特点是通过 加权和对特征进行线性变换(linear transformation),并通过偏置项来进行平移(translation)。
仿射变换的特点
高亮 🔗
常数 1 2 不会带来本质的差别,但这样在形式上稍微简单一些(因为当我们对损失函数求导后常数系数为1)。
为什么添加一个1/2系数
高亮 🔗
像线性回归这样的简单问题存在解析解,但并不是所有的问题都存在解析解。解析解可以进行很好的数学分 析,但解析解对问题的限制很严格,导致它无法广泛应用在深度学习里。
为什么解析解的泛用性不高
高亮 🔗
在训练了预先确定的若干迭代次数后(或者直到满足某些其他停止条件后),我们记录下模型参数的估计值, 表示为wˆ , bˆ。但是,即使我们的函数确实是线性的且无噪声,这些估计值也不会使损失函数真正地达到最小 值。
为什么不能到达最小值
得到最小值是一个收敛的过程
只有在无限步数情况下,才能做到真正的收敛
高亮 🔗
事实上,更难做到的是找到一组参数,这组参数能够在我们从未见过的数据上实现较低的 损失,这一挑战被称为泛化(generalization)。
什么是泛化
高亮 🔗
在训练我们的模型时,我们经常希望能够同时处理整个小批量的样本。为了实现这一点,需要我们对计算进 行矢量化,从而利用线性代数库,而不是在Python中编写开销高昂的for循环。
for循环的开销高,很大一部分因为全局解释器锁(GIL)
Python 的 GIL 限制了多线程并行执行 CPU 密集型任务,即使使用多线程的 for 循环也无法充分利用多核性能。
高亮 🔗
对于线性回归,每个输入都与每个输出(在本例中只有一个输出)相连,我们将这种变换(图3.1.2中的输出 层)称为全连接层(fully‐connected layer)或称为稠密层(dense layer)
稠密层定义
高亮 🔗
虽然飞机可能受到鸟类的启发,但几个世纪以来,鸟类学并不是航空创新的主要驱动力。同样地,如今在深 度学习中的灵感同样或更多地来自数学、统计学和计算机科学。
几马赫的飞机与鸟类 区别极大
鸟类学早就不是航空创新的驱动力
高亮 🔗
找到最优值b的解析解
average x
高亮 🔗
推导出使用平方误差的线性回归优化问题的解析解。为了简化问题,可以忽略偏置b(我们可以通过 向X添加所有值为1的一列来做到这一点)。 1. 用矩阵和向量表示法写出优化问题(将所有数据视为单个矩阵,将所有目标值视为单个向量)。 2. 计算损失对w的梯度。 3. 通过将梯度设为0、求解矩阵方程来找到解析解。 4. 什么时候可能比使用随机梯度下降更好?这种方法何时会失效?
嗯,我现在要推导使用平方误差的线性回归的解析解,而且忽略偏置项b,这时候可以通过给X矩阵加一列全1的来处理,不过题目里说现在要忽略b,也就是不需要考虑偏置项。所以问题分四个部分,先写出优化问题的矩阵向量形式,然后计算梯度,接着解方程得到解析解,最后比较什么时候用这个比SGD好,什么时候失效。
首先第一个问题,用矩阵和向量表示法写出优化问题。线性回归的平方误差损失函数通常是最小化所有样本的预测值和真实值的差的平方和。假设我们有数据集X,其中每个样本是一个行向量吗?或者列向量?这里可能需要明确数据矩阵的排列方式。通常,在机器学习中,数据矩阵X是n×d的,n是样本数,d是特征数。每个样本是一行,所以X的每一行是一个样本的特征向量。而目标值y是n维的向量。参数w是d维的向量,因为没有偏置项b,所以模型是y_pred = Xw。那平方误差损失就是各个样本的预测值与真实值的差的平方之和,即每个元素是(y_i - x_i w)^2,总和起来。所以用矩阵形式的话,可以写成 (y - Xw)^T (y - Xw) ,然后要最小化这个式子。对吧?
所以优化问题就是最小化 ||y - Xw||²,也就是min_w (y - Xw)^T (y - Xw)。这应该就是第一个问题的答案。
接下来第二个问题,计算损失对w的梯度。损失函数是L(w) = (y - Xw)^T (y - Xw)。展开的话,等于y^T y - y^T X w - w^T X^T y + w^T X^T X w。不过,可能更简单的做法是利用矩阵微积分的规则来计算梯度。例如,对于函数f(w) = (y - Xw)^T (y - Xw),求梯度df/dw。根据矩阵求导的知识,假设这里w是列向量,那么导数应该是这样的:首先展开式子,可以得到y^T y - 2 y^T X w + w^T X^T X w。这时候,梯度就是导数。对于线性项,梯度是-2 X^T y,二次项的梯度是2 X^T X w。所以整体的梯度是-2 X^T y + 2 X^T X w。或者,可以写成2 X^T (Xw - y)。对吗?
或者另一种方法,考虑损失函数L = (Xw - y)^T (Xw - y),对w求导。因为导数的规则是,对于向量a,da^T a/d a = 2a。这里a = Xw - y,所以导数应该是2 (Xw - y)^T X,但这里是关于w的梯度,所以转置一下得到梯度向量是2 X^T (Xw - y)。对的,这样对吗?是的,这样的话梯度向量是2 X^T (Xw - y),所以梯度为2 X^T X w - 2 X^T y。所以第二个问题的答案应该是梯度等于2 X^T (Xw - y),或者写成这样。
第三个问题,将梯度设为0,解方程。即令梯度等于0,得到2 X^T X w - 2 X^T y = 0,两边除以2得到X^T X w = X^T y。这时候,如果X^T X是可逆的,那么w的解就是(X^T X)^{-1} X^T y。这就是解析解,也就是正规方程的解。但如果X^T X不可逆怎么办?这个时候可能需要用伪逆,或者可能存在多个解,但题目这里可能假设X是满秩的,所以直接给出逆矩阵的存在下的解。
所以第三个问题答案就是w = (X^T X)^{-1} X^T y。不过需要注意,这里假设X^T X是可逆的,也就是X的列满秩,也就是说特征之间没有线性相关性,且样本数n≥特征数d。如果不满秩的话,可能无法求逆,这时候需要用伪逆或者其他方法。不过题目可能只要给出这个表达式即可。
第四个问题,什么时候解析解可能比随机梯度下降更好?这个方法什么时候失效?
解析解不需要迭代,直接计算得到,所以在样本量不是特别大的情况下,或者特征数不太多的时候,计算会比较快。因为当n和d比较大的时候,计算X^T X的逆可能会很耗时,尤其是当d很大的时候,因为计算逆矩阵的时间复杂度是O(d^3),如果d是上万的,那么计算会很困难。这时候可能随机梯度下降更有效,因为每次迭代的时间复杂度较低。所以当特征数d比较小,或者样本数n也不是特别大的时候,解析解更好,因为可以精确得到解,不需要调学习率等参数,也没有迭代次数的问题。而当d很大的时候,或者X^T X是奇异矩阵的时候(这时候无法求逆),或者数据量太大导致内存无法存储整个X矩阵的时候,这时候无法使用解析解,必须用梯度下降或者随机梯度下降等方法。比如,当X^T X不可逆时,解析解不存在,这时候可能需要正则化,或者使用伪逆,或者采用数值方法。所以失效的情况包括矩阵X^T X不可逆,或者计算逆矩阵的计算成本太高的时候。
总结一下:
-
优化问题:min_w ||y - Xw||²,即最小化(y - Xw)^T (y - Xw)。
-
梯度:梯度是2 X^T (Xw - y)。
-
解析解:w = (X^T X)^{-1} X^T y。
-
当d较小且X^T X可逆时,解析解更高效;当d很大、矩阵不可逆或数据量太大无法加载到内存时,解析解失效,适合用SGD。
过程中需要确认矩阵的维度是否正确,例如X是n×d的矩阵,w是d×1的向量,y是n×1的向量,所以Xw是n×1,和y同维度,相减没问题。X^T X是d×d的矩阵,计算逆矩阵是可能的。梯度计算是否正确,以及什么时候梯度下降更优需要考虑计算复杂度和实际应用场景。
可能的错误点:在梯度计算时符号是否正确。比如,损失函数展开后的导数是正确的吗?比如,原式是(y - Xw)^T (y - Xw),展开后是y^T y - 2 y^T X w + w^T X^T X w。对w求导的话,梯度是-2 X^T y + 2 X^T X w,等于2 X^T X w - 2 X^T y,也就是2 X^T (Xw - y),所以对的。
另一个需要注意的地方是,当忽略偏置项时,是否需要真的添加一列1?题目中说可以通过添加一列1来忽略b,但问题现在要求忽略b,所以原来的X是没有这一列的。所以在问题中,X已经被处理过,或者不需要处理,直接当作没有偏置项的情况,因此参数只有w,而X的维度是n×d。因此在推导的时候,不考虑b的存在,直接模型是y = Xw。
综上所述,各个问题的答案应该正确。
-
优化问题的矩阵表示:
目标是最小化平方误差损失,可以表示为:
[
\min_{\mathbf{w}} |\mathbf{y} - \mathbf{X}\mathbf{w}|^2
]
其中,(\mathbf{X}) 是 (n \times d) 的数据矩阵(每行一个样本),(\mathbf{y}) 是 (n \times 1) 的目标向量,(\mathbf{w}) 是 (d \times 1) 的权重向量。 -
损失对 (\mathbf{w}) 的梯度:
损失函数为 (L(\mathbf{w}) = (\mathbf{y} - \mathbf{X}\mathbf{w})^\top (\mathbf{y} - \mathbf{X}\mathbf{w})),其梯度为:
[
\nabla_{\mathbf{w}} L = 2\mathbf{X}^\top (\mathbf{X}\mathbf{w} - \mathbf{y})
] -
解析解:
令梯度为零,得到方程:
[
\mathbf{X}^\top \mathbf{X} \mathbf{w} = \mathbf{X}^\top \mathbf{y}
]
若 (\mathbf{X}^\top \mathbf{X}) 可逆,则解析解为:
[
\mathbf{w} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}
] -
解析解与随机梯度下降的比较:
- 解析解更优的情况:
当特征数 (d) 较小且 (\mathbf{X}^\top \mathbf{X}) 可逆时,解析解直接计算高效且精确,无需调参或迭代。
- 解析解失效的情况:
1. 计算不可行:当 (d) 很大时,计算 ((\mathbf{X}^\top \mathbf{X})^{-1}) 的时间复杂度 (O(d^3)) 过高。
2. 矩阵不可逆:当 (\mathbf{X}) 列不满秩(存在共线性)时,需引入正则化或使用伪逆。
3. 内存限制:数据量过大无法加载到内存时,需用随机梯度下降等在线方法。
答案总结:
- 优化问题:(\min_{\mathbf{w}} |\mathbf{y} - \mathbf{X}\mathbf{w}|^2)
- 梯度:(\nabla_{\mathbf{w}} L = 2\mathbf{X}^\top (\mathbf{X}\mathbf{w} - \mathbf{y}))
- 解析解:(\mathbf{w} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y})(若可逆)
- 解析解适用于小规模、满秩数据;失效于高维、共线或大数据场景。
高亮 🔗
提出一种随机梯度下降算法来解决这个问题。哪里可能出错?(提示:当我们不断更新参数时,在 驻点附近会发生什么情况)请尝试解决这个问题。
如果参数调整粒度过大,可能在驻点位置打转,刚开始时,参数调整粒度较大,后面参数调整粒度较小
高亮 🔗
features, labels = synthetic_data(true_w, true_b, 1000)
features就是X,labels就是y
高亮 🔗
yield features[batch_indices], labels[batch_indices]
yield与return类似但不同
| 特性 / 关键字 | yield | return |
| 返回值次数 | 多次返回值,每次产生一个结果 | 仅返回一次,函数立即终止 |
| 内存占用 | 低(逐次生成,不保存完整结果) | 高(需一次性存储所有结果) |
| 函数类型 | 生成器函数(可迭代) | 普通函数 |
| 执行状态 | 暂停并保留当前状态,下次继续执行 | 完全退出函数,状态销毁 |
| 典型应用场景 | 大数据分批处理、流式数据、惰性计算 | 小数据集、一次性计算结果 |
| 调用方式 | 通过 next () 或 for 循环逐步获取 | 直接获取全部结果 |
高亮 🔗
with torch.no_grad():
| Context-manager that disables gradient calculation. | | Disabling gradient calculation is useful for inference, when you are sure | that you will not call :meth:Tensor.backward(). It will reduce memory | consumption for computations that would otherwise have requires_grad=True.
高亮 🔗
如果我们将权重初始化为零,会发生什么。算法仍然有效吗?
w 初始化为 0 不会导致算法失效,因为梯度下降仍能基于数据计算有效梯度并更新参数。最终模型会收敛到最优解,只是初始阶段可能需要更多迭代步骤。线性回归的有效性不依赖于参数初始值的选择,而是依赖于损失函数的凸性和优化过程的正确性。
高亮 🔗
假设试图为电压和电流的关系建立一个模型。自动微分可以用来学习模型的参数吗?
电压与电流是一个线性的模型U=IR
可以使用自动微分来学习
高亮 🔗
为什么在squared_loss函数中需要使用reshape函数?
在这个代码中,y_hat与y形状相同
而在其他可能的情况下,y_hat与y形状可能不同.为了避免形状不同导致的报错,选择使用reshape函数避免
高亮 🔗
在PyTorch中,全连接层在Linear类中定义。值得注意的是,我们将两个参数传递到nn.Linear中。第一个指 定输入特征形状,即2,第二个指定输出特征形状,输出特征形状为单个标量,因此为1。
高亮 🔗
net[0].weight.data.normal_(0, 0.01) net[0].bias.data.fill_(0)
使用Normal与fill重写
高亮 🔗
SGD实例
什么是SGD
Stochastic gradient descent
随机梯度下降
高亮 🔗
trainer.step()
梯度更新
高亮 🔗
如果将小批量的总损失替换为小批量损失的平均值,需要如何更改学习率?
new_lr=lr/batch_size
高亮 🔗
但是一般的分类问题并不与类别之间的自然顺序有关。幸运的是,统计学家很早以前就发明了一种表示分类 数据的简单方法:独热编码(one‐hot encoding)。独热编码是一个向量,它的分量和类别一样多。类别对 应的分量设置为1,其他所有分量设置为0。在我们的例子中,标签y将是一个三维向量,其中(1, 0, 0)对应于 “猫”、(0, 1, 0)对应于“鸡”、(0, 0, 1)对应于“狗”: y ∈ {(1, 0, 0), (0, 1, 0), (0, 0, 1)}.
什么是独热编码
one-hot encoding
高亮 🔗
正如我们将在后续章节中看到的,在深度学习中,全连接层无处不在。然而,顾名思义,全连接层是“完全”连 接的,可能有很多可学习的参数。具体来说,对于任何具有d个输入和q个输出的全连接层,参数开销为O(dq), 这个数字在实践中可能高得令人望而却步。幸运的是,将d个输入转换为q个输出的成本可以减少到O( dq n ),其 中超参数n可以由我们灵活指定,以在实际应用中平衡参数节约和模型有效性 (Zhang et al., 2021)。
如何使用超参数减少全连接层的开销
高亮 🔗
然而我们能否将未规范化的预测o直接视作我们感兴趣的输出呢?答案是否定的。
将线性层的输出直接 视为概率时存在一些问题:
一方面,我们没有限制这些输出数字的总和为1。
另一方面,根据输入的不同,它 们可以为负值。
这些违反了 2.6节中所说的概率基本公理。
softmax层其实就是规范化预测的结果,使它能够符合概率论的三条基本定理
高亮 🔗
softmax函数能够将未规范化的预测变换为非负数并且总和为1,同时让模型保持可导的性质。
图片
softmax使用e^{o_j}形式的指数函数,进行标准化
高亮 🔗
尽管softmax是一个非线性函数,但softmax回归的输出仍然由输入特征的仿射变换决定。因此,softmax回 归是一个线性模型(linear model)。
为什么是一个线性模型?
Softmax 回归的线性本质源于其对输入特征的仿射变换的直接依赖。尽管 softmax 函数引入了非线性归一化,但模型的分类能力完全由线性组合决定,因此它属于线性模型。这一特性使其适用于线性可分问题,但无法捕捉复杂非线性关系。
图片
交叉熵损失的定义
高亮 🔗
由于y是一个 长度为q的独热编码向量,所以除了一个项以外的所有项j 都消失了。
图片
交叉熵损失函数的导数与softmax函数之间的关系
高亮 🔗
我们可以把交叉熵想象为“主观概率为Q的观察者在看到根据概率P 生成的数据时的预期惊异”。 当P = Q时,交叉熵达到最低。在这种情况下,从P 到Q的交叉熵是H(P, P ) = H(P )。
高亮 🔗
softmax运算获取一个向量并将其映射为概率。
softmax运算的结果是一个向量,只是在解释的时候.将其变换为概率的形式
高亮 🔗
softmax回归
softmax为什么是回归模型而不是分类模型?
任务类型(分类 / 回归)和模型方法(线性模型 / 树模型 / 神经网络)
softmax的命名并不是采用了任务类型的方式,而是模型放方法
softmax 的任务是分类,但建模方式延续了广义线性模型的框架,因此被称为 “回归”
高亮 🔗
b = torch.zeros(num_outputs, requires_grad=True)
b = torch.zeros(size=(1,num_outputs), requires_grad=True)的省略写法
高亮 🔗
X_exp = torch.exp(X) partition = X_exp.sum(1, keepdim=True) return X_exp / partition # 这里应用了广播机制
对X_exp与 partition的形状不同,使用广播机制可以实现X_exp的每一位都被partition除
高亮 🔗
y = torch.tensor([0, 2]) y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]]) y_hat[[0, 1], y]
第三行实现索引配对
- 索引规则
第一个索引列表 [0, 1]:对应行索引,即 y_hat 的第 0 行和第 1 行。第二个索引列表 y:对应列索引,即 y_hat 的第 0 列和第 2 列(因为 y = [0, 2])。 - 元素配对
PyTorch 会将两个索引列表按位置配对,生成以下坐标对:
第 0 行,第 0 列 → y_hat[0, 0] = 0.1第 1 行,第 2 列 → y_hat[1, 2] = 0.5
3. 输出结果
最终返回一个一维张量,包含这两个元素:
python
Copy
tensor([0.1000, 0.5000])
高亮 🔗
def cross_entropy(y_hat, y): return - torch.log(y_hat[range(len(y_hat)), y])
range(len(y_hat))就是取行索引
y_hat[range(len(y_hat)),y]与y_hat[[0, 1], y]实际上是相同的
高亮 🔗
本节直接实现了基于数学定义softmax运算的softmax函数。这可能会导致什么问题?提示:尝试计 算exp(50)的大小。
没有处理一些特别大的异常值
coner case 需要多多考虑
高亮 🔗
本节中的函数cross_entropy是根据交叉熵损失函数的定义实现的。它可能有什么问题?提示:考虑对 数的定义域。
没有避免y_hat.argmax(dim=1)中,存在负数项
高亮 🔗
4. 返回概率最大的分类标签总是最优解吗?例如,医疗诊断场景下可以这样做吗?
并不是,只是在这个种子的情况下的局部最优解
医疗场景肯定不可以
高亮 🔗
假设我们使用softmax回归来预测下一个单词,可选取的单词数目过多可能会带来哪些问题?
-
计算复杂度高
指数运算开销:Softmax 需要对所有候选单词的得分(logits)计算指数并归一化。若词汇量为 ,每次计算的时间复杂度为 。当
极大(如数万或数十万),这会显著拖慢训练和推理速度。 内存瓶颈:存储所有单词的得分和概率向量需要 的内存空间,可能导致显存或内存不足,尤其是在 GPU 受限的场景下。 -
模型参数爆炸
权重矩阵规模:Softmax 回归的权重矩阵维度为 ( 为输入特征维度,如隐藏层大小)。当 极大时,参数数量激增(例如 时参数达 5 千万),导致:内存占用过高,难以部署到资源受限的设备。训练时梯度计算和参数更新的效率降低。 -
训练效率低下
稀疏梯度更新:大多数单词在单个样本中不会出现,导致对应的权重参数很少被更新(梯度稀疏),影响模型收敛速度。类别不均衡:高频词占据主导地位,低频词因样本不足难以学习,模型可能偏向预测常见词而忽略合理但低频的候选词。 -
梯度传播问题
梯度消失 / 爆炸:大规模权重矩阵可能导致反向传播时梯度不稳定,需依赖精细的参数初始化(如 Xavier/He 初始化)或梯度裁剪(gradient clipping)来缓解。噪声干扰:大量无关单词的梯度可能引入噪声,影响模型对关键特征的捕捉。 -
预测偏向高频词
Softmax 概率倾斜:Softmax 倾向于放大高分值的概率,而词汇量过大时,高频词更容易获得高初始得分(如通过偏置项),导致模型过度预测常见词(如 “the”、“is”),降低生成多样性。
高亮 🔗
我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制,使其能处理更普遍的函数关系类型。
如何突破线性模型的限制
图片
权重与偏置的形状
图片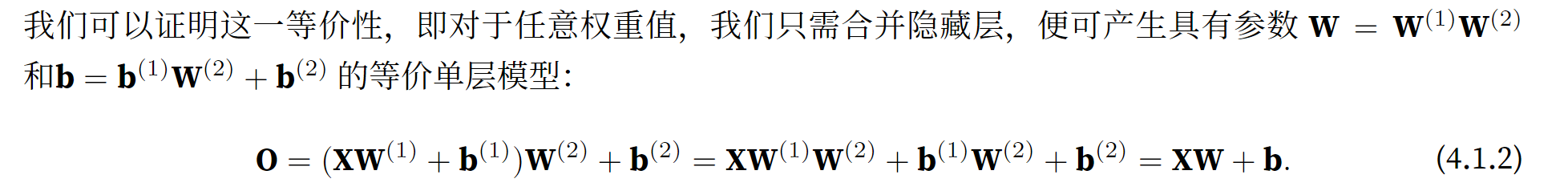
不使用激活函数的多层感知机和单层感知机有区别吗?
没有
高亮 🔗
多层感知机可以通过隐藏神经元,捕捉到输入之间复杂的相互作用,这些神经元依赖于每个输入的值。我们 可以很容易地设计隐藏节点来执行任意计算。例如,在一对输入上进行基本逻辑操作,多层感知机是通用近 似器。即使是网络只有一个隐藏层,给定足够的神经元和正确的权重,我们可以对任意函数建模,尽管实际 中学习该函数是很困难的。神经网络有点像C语言。C语言和任何其他现代编程语言一样,能够表达任何可计 算的程序。但实际上,想出一个符合规范的程序才是最困难的部分。 而且,虽然一个单隐层网络能学习任何函数,但并不意味着我们应该尝试使用单隐藏层网络来解决所有问题。 事实上,通过使用更深(而不是更广)的网络,我们可以更容易地逼近许多函数。我们将在后面的章节中进 行更细致的讨论
单隐层网络能够解决所有问题吗
多隐层网络能够解决所有问题吗
高亮 🔗
ReLU(x) = max(x, 0).
ReLU激活函数的定义
高亮 🔗
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True) y = torch.relu(x) d2l.plot(x.detach(), y.detach(), ‘x’, ‘relu(x)’, figsize=(5, 2.5))
为什么这里画图需要使用detach()?
requires_grad=True 导致存在计算图
而画图的时候,是不需要计算图的,纯数值就够用了
使用detach(),去除计算图
高亮 🔗
当输入为负时,ReLU函数的导数为0,而当输入为正时,ReLU函数的导数为1。注意,当输入值精确等于0时, ReLU函数不可导。在此时,我们默认使用左侧的导数,即当输入为0时导数为0。
对于ReLU导数的处理
高亮 🔗
y.backward(torch.ones_like(x), retain_graph=True) d2l.plot(x.detach(), x.grad, ‘x’, ‘grad of relu’, figsize=(5, 2.5))
torch.ones_like(x)有什么作用?
给定backward时候的权重参数
torch.ones_like(x) 生成与 x 形状相同的全 1 张量,表示对 y 的每个元素赋予权重 1。反向传播时,PyTorch 会计算以下标量的梯度:
weighted_sum = sum(y_i * 1) # 对 y 的所有元素求和
然后对 weighted_sum 求 x 的梯度。
图片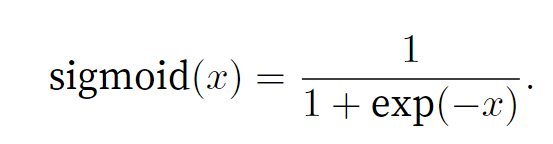
sigmoid 定义
高亮 🔗
然而,sigmoid在隐藏层中已经较少使用,它在大部分时候被更简单、 更容易训练的ReLU所取代。
为什么ReLU比sigmoid 更加简单且容易训练?
从开销的角度
sigmoid使用了exp()函数,而exp()函数的开销极大,进行一次exp计算,可以进行上百次加法运算.
图片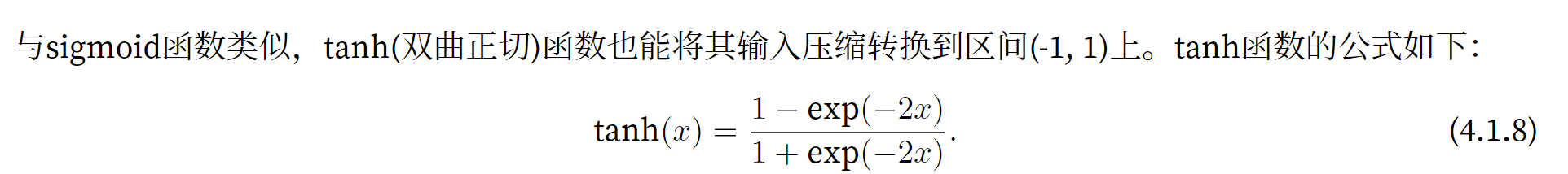
tanh激活函数定义
高亮 🔗
当我们有简单的模型和大量的数据时,我们期望泛化误差与训练误差相近。当我们有更复杂的模型和更少的 样本时,我们预计训练误差会下降,但泛化误差会增大。
高亮 🔗
当训练数据稀缺时,我们甚至可能无法提供足够的数据来构成一个合适的验证集。这个问题的一个流行的解 决方案是采用K 折交叉验证。这里,原始训练数据被分成K 个不重叠的子集。然后执行K 次模型训练和验证, 每次在K − 1个子集上进行训练,并在剩余的一个子集(在该轮中没有用于训练的子集)上进行验证。最后, 通过对K 次实验的结果取平均来估计训练和验证误差。
K折交叉验证定义
高亮 🔗
如果不对多项式特征xi进行标准化(1/i!),会发生什么事情?能用其他方法解决这个问题吗?
梯度过大,不利于SGD
图片
为什么不能通过调整特征个数控制模型复杂度