矩估计
数理统计中的矩估计法的计算
- {计算总体矩 EX}
- {总体矩=样本矩,
} 得到方程组 - 根据 2 的方程组,{求解未知参数}
Q: 矩估计中, 如果 EX=c, 而不是一个关于未知参数的函数,
无法通过连立
A: 按顺序使用更高阶的 k 阶矩 (二阶、三阶…), 直到找到一个包含未知参数的总体矩.
连立总体矩=样本矩,
矩估计法中使用的矩可以是{原点矩} 也可以是{中心矩}
Q: 矩的阶数与未知参数个数的关系
A: 有
最大似然估计
似然函数
- 离散型分布律为
{ } - 连续型概率密度为
{ }
估计量的评价标准:
- 无偏: {估计量的数学期望
存在, 且 , 则称 是 的无偏估计} - 有效: {估计量
与 都是 的无偏估计量. 若 则称 更有效} - 一致: {当
时, 估计量 依概率收敛于 (即对任意 , 有 ) 则称 是 的一致 (相和) 估计量}
一致性的判断
Q: 单个参数
A: 1. 总体矩:
2. 样本矩:
3. 总体矩=样本矩, 即
求最大似然估计的过程实际上是在寻找{
最大似然估计的求解过程 (离散型与连续型)
- 写出似然函数
- 求
- 判断
- 有解, 解出参数
- 无解, 讨论 (常在边界点), 得到参数

- 有解, 解出参数
假设检验
假设检验的两类错误
第一类错误:{c1:原假设
第二类错误:{c1:原假设
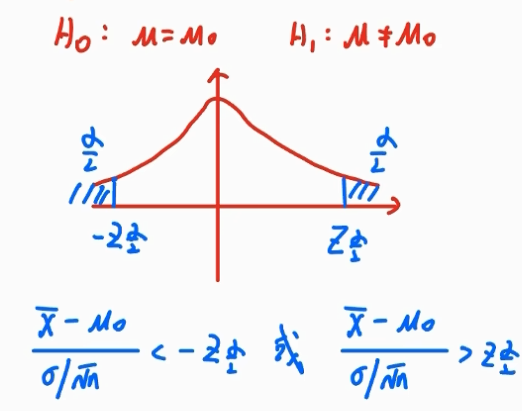
双边假设检验:形如
单边假设检验:
形如
形如
Q:
A: 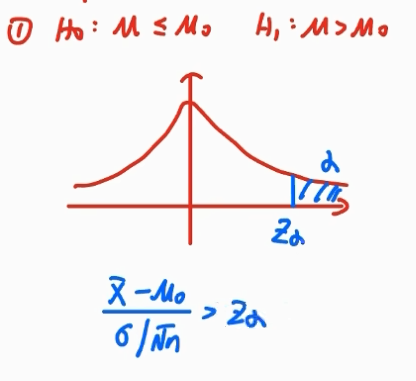
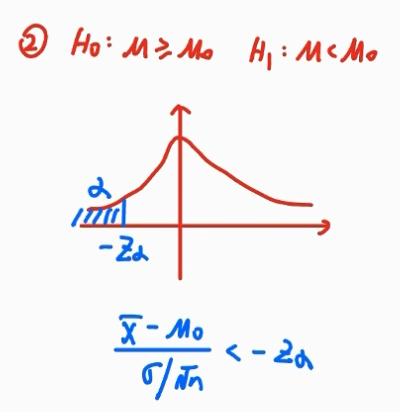
Q:
A: