Q: 为什么不定积分 (原函数) 这么强调定义域,
而定积分不怎么强调定义域?
A: 不定义积分与定积分的概念有所不同
从不定积分 (原函数) 的定义看, 要求区间内任意一点都有
定积分计算的是面积. 不要求区间内任意一点都有
原函数
连续决定了, 即使是
注意这里是原函数, 不是变限积分, 性质有所不同
原函数 (不定积分) 存在性定理 (1)
连续函数{必有}原函数
Q: 如果函数
A: 可导, 且
证明如果函数
显而易见,
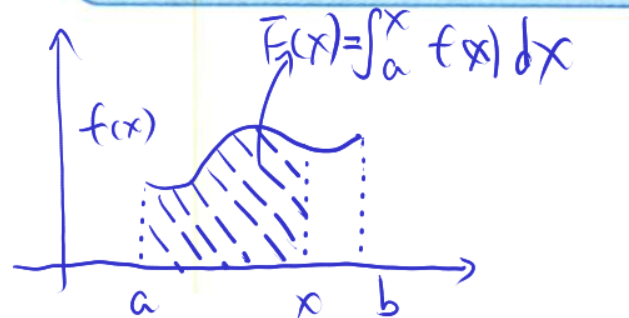
对于
对于
对于
Q: 为什么连续函数于闭区间上必可积
A: 事实上, 函数于闭区间内连续, 就一定是有界的
例如
闭区间取不到
那么于
函数
黎曼积分的框架下,
Q:
A: 可导必连续, 连续必可积, 可积必有界
反过来就不行了
Q: 有界必可积吗?
A: 错误的, 有界并不是充分条件, 只是必要条件
以狄利克雷函数为例子
Q: 为什么有界是可积的必要条件, 不是充分条件
A: 必要性: 可积是黎曼可积, 要求被积函数有界
非充分性: 以狄利克雷函数为例子, 有界但是不可积
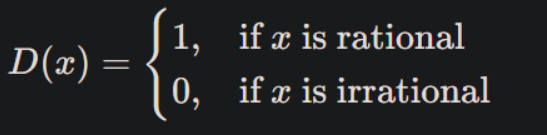
黎曼积分存在 (定积分存在) 的两个必要条件
- {积分区间有限}
- {被积函数有界}
可积是指{黎曼}积分{存在}, 原函数, 反常积分{不一定存在}
函数
可积指的是能够进行定积分运算, 定积分存在的必要条件是函数有界
用函数的有界性证明
得证
Q: 对于可导函数
有界区间上
无穷区间上
A: 有界区间上
无穷区间上
Q: 为什么对于可导函数
有界区间上
A: 证明
原函数 (不定积分) 存在性定理 (2)
根据间断点判断原函数情况
有{第一类间断点}或者{无穷间断点}的函数
有{振荡间断点}的函数
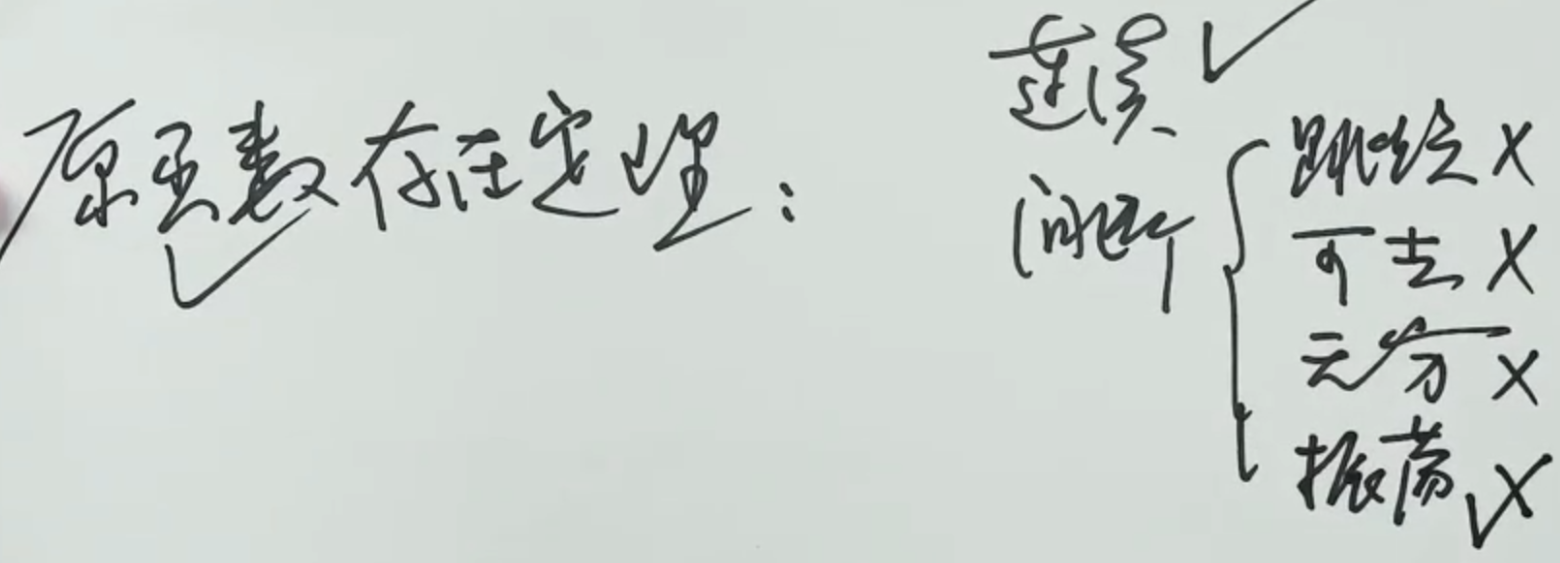
可导函数
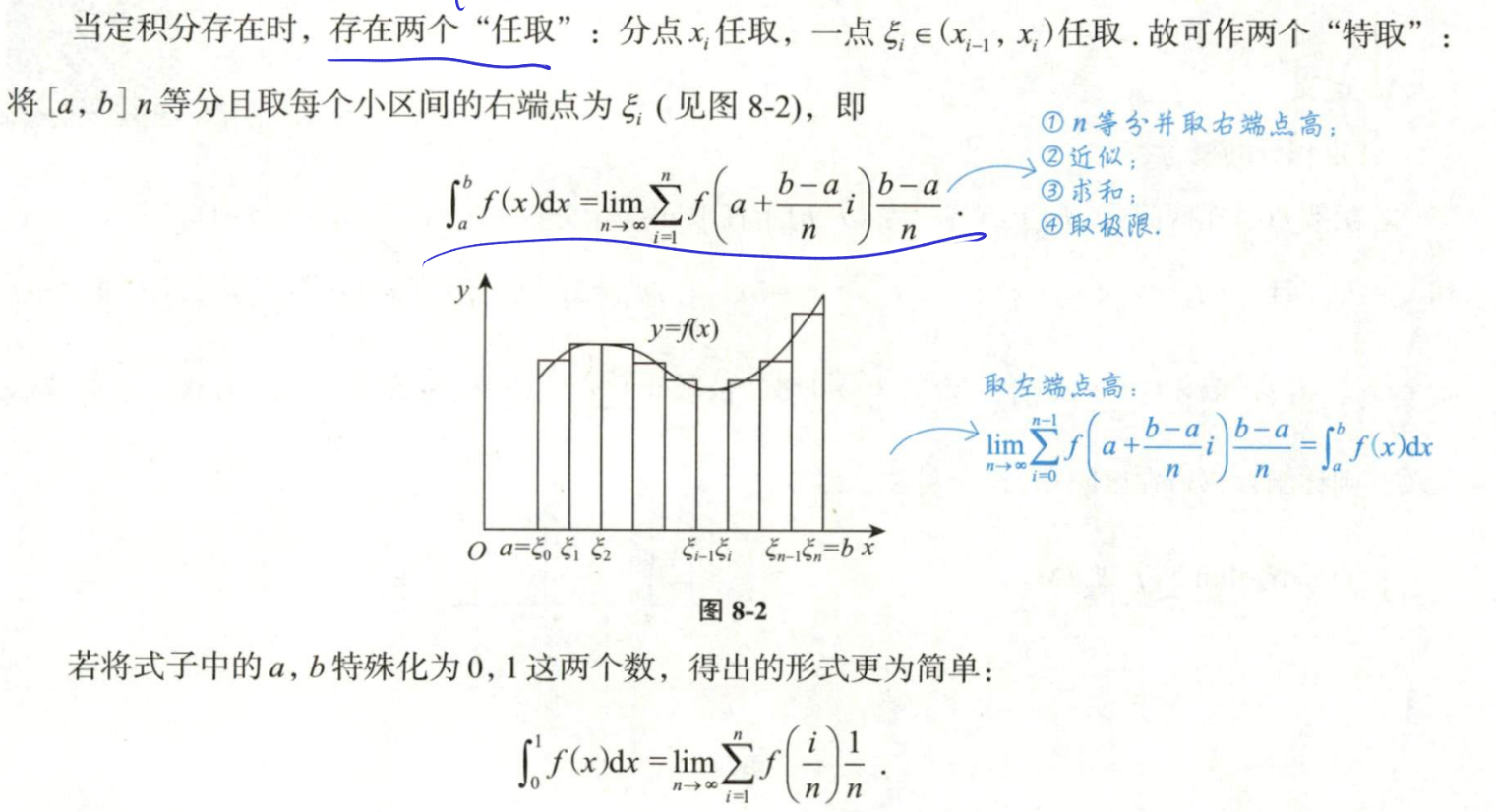
Q: 数列与定积分的转化, 找可爱因子
A: 将一个数列形式的式子转化为定积分的形式
找到四个关键
的范围 定积分的积分区域
积分的保号性
若在区间
Q: 积分的估值定理
A:
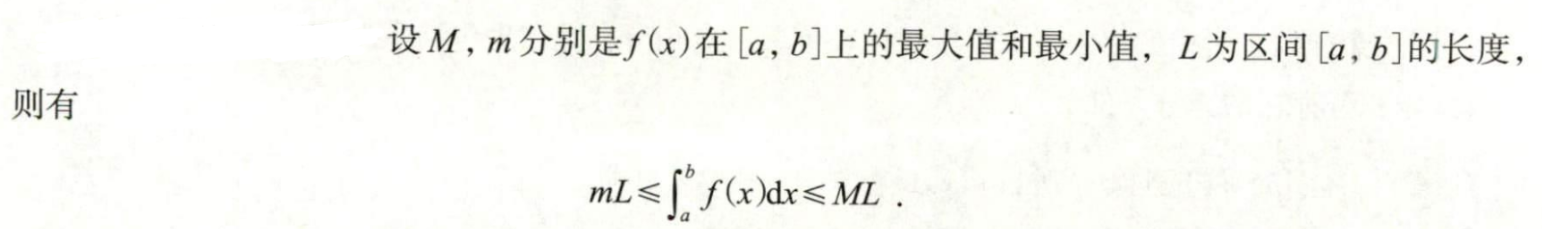
Q: 积分中值定理
A: 设
Q: 从几何的角度理解积分中值定理
A: 将原来的面积变为一个矩形的面积
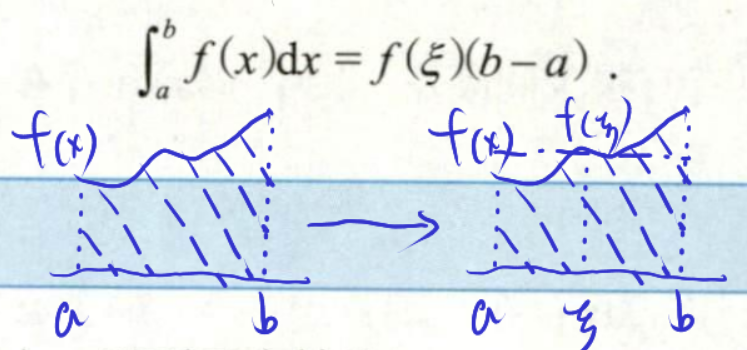
拉格朗日中值定理证明积分中值定理
定理 (积分中值定理): 如果函数
证明:
- 构造辅助函数.
令, 其中 . - 验证拉格朗日中值定理的条件.
- 因为
在 上连续, 根据微积分基本定理, 变上限积分函数 在 上是可导的, 其导数为 . - 一个函数在区间上可导, 则它必然在该区间上连续. 因此,
在 上连续, 在 内可导. - 至此,
满足在区间 上使用拉格朗日中值定理的所有条件.
- 因为
- 应用拉格朗日中值定理.
根据该定理, 在开区间内至少存在一点 , 使得:
- 代入并化简.
- 根据
的定义, 我们有 . - 同样地,
. - 根据第 2 步的结论, 我们有
.
将这三项代入上面的等式, 得到:
即:
- 根据
- 结论.
由于定积分的值与积分变量的符号无关, 我们可以将写成 :
证明完毕.
Q: 定积分的值与字母无关说的是什么
A: 当定积分存在时, 换自变量对定积分的结果没有影响
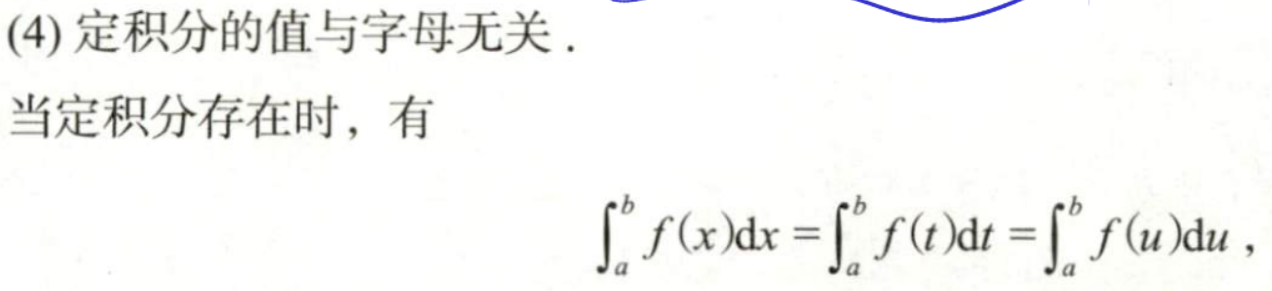
定积分存在定理的充分条件
若
若
若
Q:
A: 连续性并不是必要条件. 有限个间断点, 且有上下界的不连续函数也有定积分
“可积的”, 通常是指这个函数在某个区间上可以计算{定积分}.
Q: 定积分与原函数的区别
A: 原函数是从函数角度求解, 但大部分函数都是没有原函数的. 只有少部分能够满足原函数存在定理.
定积分则超出了函数角度, 而是从面积来看, 不论一个函数是否有原函数, 只要他连续且有界就一定有与
若
若
Q: 为什么不论
A: 要证明
因为 f(x) 在 x₀ 处只有一个跳跃间断点,所以在包含 x₀ 的任意一个小的闭区间内,f(x) 是有界的。即存在一个常数 M > 0 和 δ > 0,使得对于所有 t ∈ (x₀ - δ, x₀ + δ),都有 |f(t)| ≤ M。
现在,我们考虑极限 lim(x→x₀)。我们可以只看 x 在 (x₀ - δ, x₀ + δ) 内的情况。
根据定积分的基本性质:
因为 |f(t)| ≤ M,所以:
于是我们得到不等式:
当 x → x₀ 时,|x - x₀| → 0,所以 M \cdot |x - x₀| → 0。
根据夹逼定理 (Squeeze Theorem),我们得出结论:
这也就证明了 lim(x→x₀) F(x) = F(x₀),即 F(x) 在 x₀ 点是连续的。T
Q: 如何理解若
A: 跳跃间断点性质
由于
而从不同方向靠近,
但是极限具有唯一性, 不同的
且左右的极限为
Q:
A: 不对称
正负无穷不是一个具体的实数, 而是一群无穷大的数组成的集合.
只有
这时候, 积分区间是无穷大且对称
Q: 什么是瑕点? (反常积分概念)
A: 设瑕点为 无界
Q: 判断积分敛散性时候, 出现多个瑕点怎么处理?
A: 一个积分中只能有一个瑕点, 如果有多个瑕点, 则进行拆分计算.
只有当每个小积分区间都收敛时, 整体才收敛
反常积分敛散性判断
瑕点为
寻找一个函数
根据c的不同取值,与
Q: 无穷区间的不等式缩放判别.
A: 
注意⚠️ 比较判别法要求两个函数都要{

- 非负函数的积分具有单调性, 只能单调增加. 这样才能判定, 大的收敛小的必收敛, 小的发散, 大的必发散
- 非负使得不存在积分抵消的情况. 如有积分抵消, 判别法可能不成立
Q: 敛散性除法极限判别
A: 
Q: 被积函数无界的不等式缩放判别法,
比较判别法
A: 
被积函数无界的不等式缩放判别法,
敛散性判别究极无敌重要结论
为什么敛散性判别重要结论要用
在
在
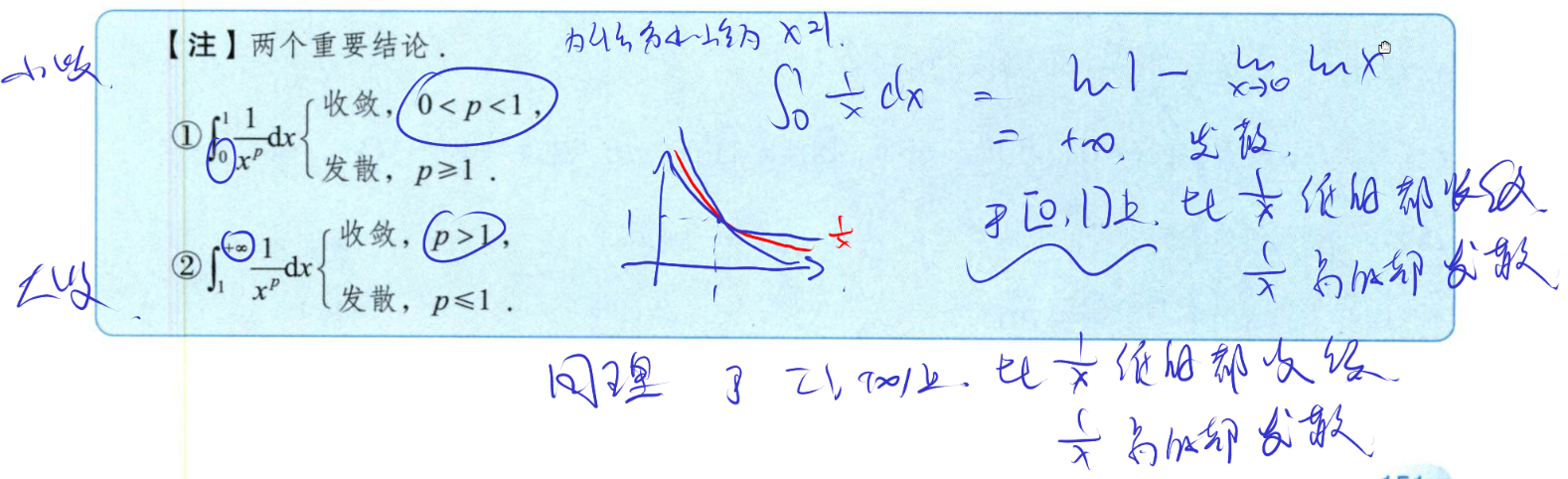
Q: 从接近速度的角度理解敛散性判别重要结论
A: 对于
同理
对于
Q: 对敛散性重要结论如何广义化? 对于
A:
由于
Q: 对敛散性重要结论如何广义化? 对于
A: 由于
因为敛散性, 奇偶函数有新的特点
对于偶函数,
对于奇函数,