🪴 l4rk's Quartz

05特征值与特征向量

10分钟阅读

特征值与特征向量

特征值与特征向量的定义
代数:{}

幂零矩阵 的特征值为{0}

Q: 为 阶单位列向量, 则 的特征值为?
A: 唯一非零特征值为 1, 剩下 个特征值为 0
秩一矩阵角度:
, 唯一非零特征值等于
特征向量角度:
,
取一个与 正交的向量 , , 存在 个线性无关的向量

若矩阵 , 则{}一定为矩阵的一个特征值

Q: 如何从几何的角度理解特征值与特征向量的定义, ?
A: A 代表了一个线性变换矩阵
为一个向量
为一个数
意为
对向量 进行 A 代表的线性变换, 得到的新向量, 仍然落在 张成的直线上
只是长度变为了原来的 倍

Q: 对于 , 如何求得特征值
A:
得到一个关于 的多项式, 解就是 的全部取值

Q: 利用条件给定的特殊关系求 A 的特征值
例如
A:
解的集合为
则 的实际特征值为该集合的子集
即 特可能全为 , 也可能全为 , 也可能既有 也有

Q: 为什么可以使用 , 求出 的特征值
A: 先统一左右的格式
左边为矩阵向量乘法, 右边为向量数乘
将右边变为矩阵向量的乘法

  1. 若
    则上式恒成立, 但是这个特征向量没有意义
  2. 若
    代数的角度: 齐次方程有非零解的情况, 便是 存在自由变量, 列不满秩, 等价于
    几何的角度: 所代表的线性变换能够将 压缩, 在当前的空间中,

设 阶矩阵 的特征值为 ,
则 {}

对于
一个确定的特征值, 对应{一个或一个以上}线性无关的特征向量
一个确定的特征向量, 对应{一个特征值}

Q: , A 形如 m*n 如何求一个确定的特征值 对应了几个线性无关的特征向量?
A: 齐次方程 的解就是 对应的特征向量
线性无关的特征向量的个数为

, 则 的特征值为{}

A 的各行元素之和均为 0, 则 A 存在一个特征值为{c1:0}, 其对应的特征向量为{c1: }

Q: 为什么 A 的各行元素之和均为 0, 则 A 存在一个特征值为 0, 其对应的特征向量为 ?
A: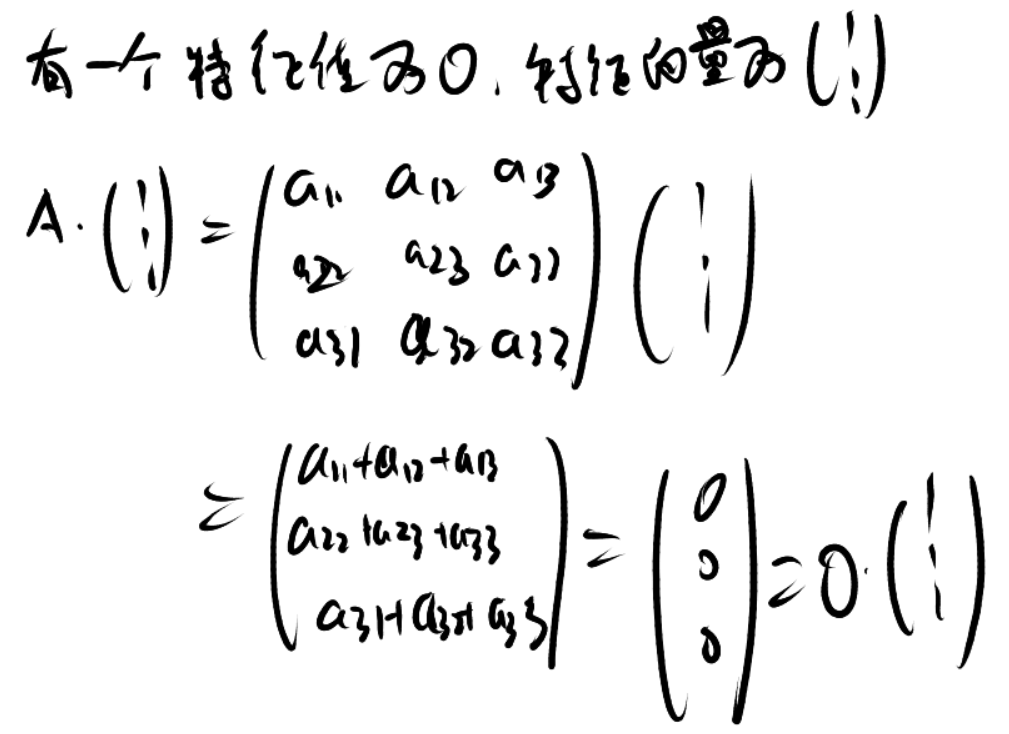

Q: 为什么不同特征值的特征向量之和不是特征向量? 用特征向量的定义证明
A: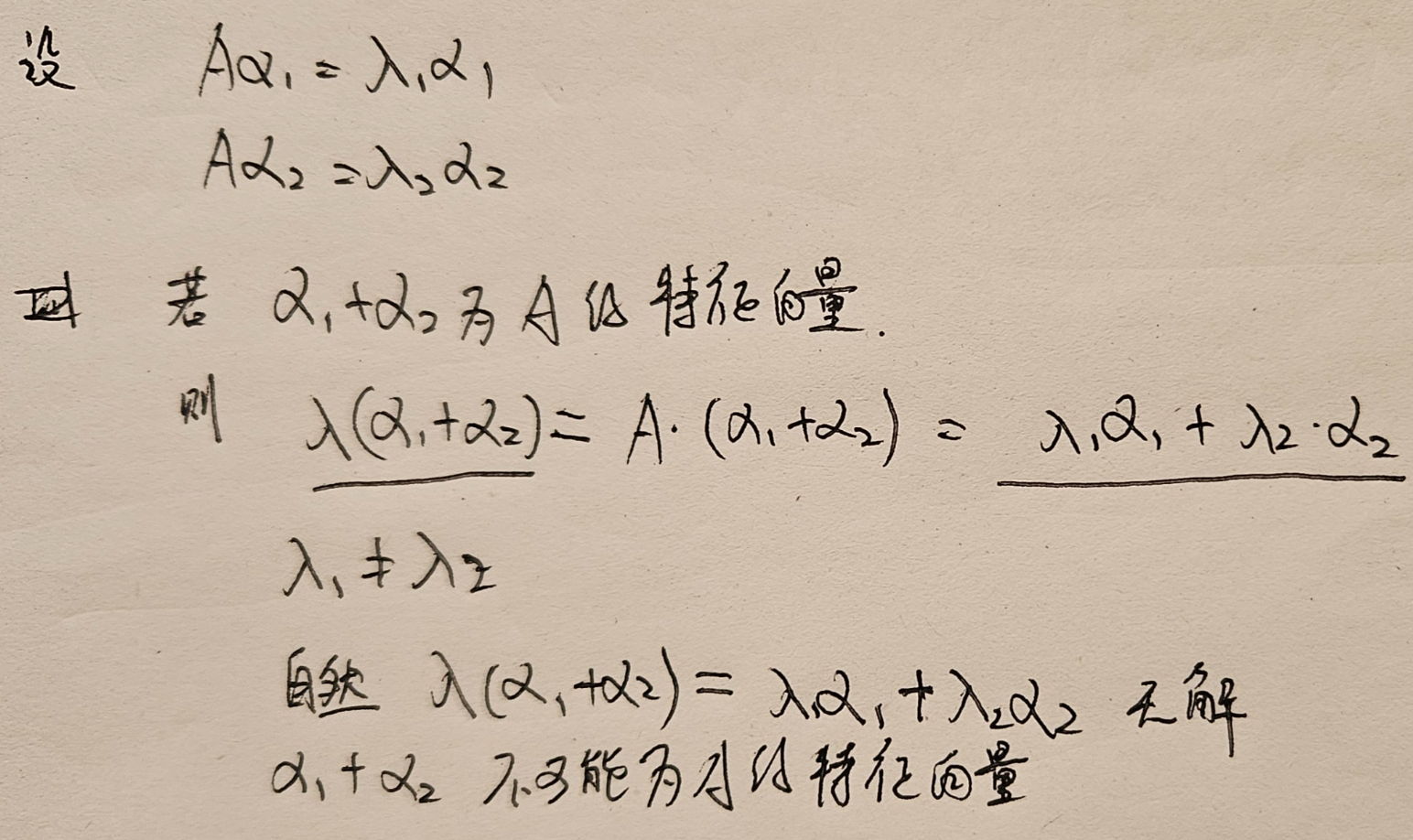

Q: 不同特征值的特征向量线性相关吗?
A: 线性无关

Q: 特征值 的代数重数>=几何重数
什么是代数重数, 什么是几何重数?
A: 代数重数: , 解= 的个数为 的代数重数
几何重数: 对应的线性无关特征向量的个数,

如何使用 A 的特征向量求得 A 的行列式?
{}

{c1: }{c2: }{c3: }{c4: }{c5: }
{c1: }{c2: }{c3: }{c4: 通常不为 }{c5: }

Q: 已知 A 的特征值为 , 如何快速求得 的特征值
A: 特征值
同理, 特征值 ,

Q: 已知 A 的特征值为 ()
求 的特征值
A:
同理,

迹

矩阵 A 的迹与特征值的关系
tr (A)={}

Q: 矩阵 A 的迹与特征值的关系
是否要求矩阵 为可对角化矩阵?
A: 不要求
任意矩阵都有这个特性

相似

矩阵相似的定义
A, B 均为 n 阶矩阵
若存在 n 阶可逆矩阵 P, 使得{}
则称

若 , 则 A, B 有相同的行列式, 秩, 特征方程, 特征值, 迹

相似的传递性
若 , , 则{}

Q: 什么是相似的感染性
A: 若 , 则

Q: 什么条件下 ?
A: A 或 B 是可逆矩阵
假设 A 为一个可逆矩阵
则有, , 符合相似的代数定义

对角化

Q: 什么是矩阵的对角化?
A: 对于矩阵 , 存在一个可逆矩阵 与对角阵
使得 成立, 即 相似于对角阵

Q: 对于 矩阵 恒等于其非零特征值的个数吗?
A: 这个结论对于可对角化矩阵是成立的
对于其他类型矩阵不成立

R (A) 与非零特征值的个数关系
{c2: A 可对角化}:{c1: r (A) = 非零特征值的个数}
{c2: A 不可对角化}:{c1: r (A) ≥ 非零特征值的个数}

相似对角化

相似对角化的定义
A 为 n 阶矩阵, 为 n 阶对角矩阵
若存在 n 阶可逆矩阵 P, 使得{}
则称 A 可相似对角化

Q: 中 与 的本质是什么?
A: 为 n 阶对角矩阵, 对角线上的每一个元素都是特征值
为 n 阶矩阵, P 的每一个列向量都是对应对角矩阵上的特征值 的特征向量 . 并且 中的所有列向量都线性无关

Q: n 阶矩阵 A 可以相似对角化的第一充要条件
A: 有 n 个线性无关的特征向量

Q: n 阶矩阵 A 可以相似对角化的第二充要条件
A: k 重特征值有 k 个特征向量 (其实就是有 n 个线性无关的特征向量)

若 A, B 均可相似对角化, 则 A 与 B 相似的充要条件是:{A 与 B 有相同的特征值}

Q: 实对称矩阵可以相似对角化吗?
A: 是的
实对称矩阵不仅可以相似对角化, 还可以正交相似对角化

若 A 为实对称矩阵, 则 r (A) 为{非零特征值的个数}

秩一矩阵 可对角化的充要条件为{}

Q: 上三角或者下三角矩阵可以相似对角化吗?
A: 上三角, 下三角一定可以相似对角化

Q: 上三角或者下三角矩阵对角线上的值和特征值有什么关系?
A:

实对称矩阵

Q: 什么样的矩阵是实对称矩阵?
A: 它是一个方阵 (Square Matrix): 即矩阵的行数和列数相等.
所有元素都是实数 (Real Numbers): 矩阵中不包含复数.
矩阵等于其自身的转置 (): 这是”对称”性质的核心.

实对称矩阵的性质

  1. 不同特征值的特征向量{正交}
  2. K 重特征值有{k}个线性无关的特征向量
  3. 一定可以{正交}相似对角化

Q: 什么是实对称矩阵 A 的正交相似对角化?
A: 存在一个正交矩阵 Q, 使得

Q: 对于矩阵 , 的值=非零特征值的个数, 在什么条件下成立?
A: 为可相似对角化矩阵

对于实对称矩阵 与某个正交矩阵 , 符合
{}={}

关系图谱