🪴 l4rk's Quartz

06一元函数微分学的应用(二)---中值定理,微分等式与微分不等式

7分钟阅读

中值定理的重要作用就是联系了{函数的差值}与{函数变化率}

涉及函数的定理: 有界与最值定理, 介值定理, 平均值定理, 零点定理
涉及导数的定理: 费马定理, 罗尔定理, 拉格朗日中值定理, 柯西中值定理, 泰勒公式
涉及积分的定理: 积分中值定理

只有{连续}(函数的性质) 函数才能使用介值定理

Q: 什么是介质定理?
A: 于 上连续, 如果有一个介于 和 之间的任意值 , 那么一定存在一个点 , 使得 , 并且

Q: 零点定理与介质定理的关系
A: 零点定理是特殊的介质定理
介质定理为: 于 上连续, 如果有一个介于 和 之间的任意值 , 那么一定存在一个点 , 使得 , 并且
当 , 异号的时候, 就是零点定理

Q: 零点定理的定义
A: 如果一个连续函数在区间的两端取值分别为正值和负值, 则在这个区间的某处, 该函数必然等于零.

Q: 零点定理区间两端的函数值如果不存在怎么办呢
A:
函数值是否存在不影响, 只要对应的左右极限存在就行

Q: 费马定理条件与结论
A: 在点 满足

  • 可导
  • 取极值 (端点不讨论)
    则

费马定理的证明
证明:
假设函数 于点 取到极大值, 那么在邻域 中, 有

因为 可导, 所以

Q: 罗尔定理条件与结论
A: 满足

  • 连续
  • 可导

  • 则存在 , 使得

Q: 条件扩展的罗尔定理
A: 满足

  • 连续
  • 可导 (可以是有限区间也可以是无限区间)
  • 或者
    结论不变

如何从图像的角度理解罗尔定理
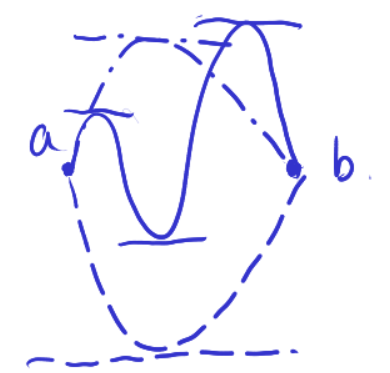
从图像角度比较好理解, 连续可导函数 的定义域 中, 左右函数值都是相等的, 不论函数中间图像如何变化, 必有一点 的导数值为

Q: 高阶罗尔定理使用
A: 只要多找几个函数值相同的点

由 两点可得
同理, 由 两点可得

同理, 由 可得
多次使用罗尔定理, 多次升阶

Q: 拉格朗日中值定理条件与结论
A: 满足

  • 连续
  • 可导
    则存在

见到{函数做差 }或者{ 与 }的时候, 要想到使用拉格朗日中值定理

如何从图像的角度理解拉格朗日中值定理

像是斜过来的罗尔定理

Q: 柯西中值定理条件与结论
A: 满足

  • 连续
  • 可导

  • 则存在 使得

Q: 柯西中值定理与拉格朗日中值定理的联系
A:

显然柯西中值定理就像把两个不同的拉格朗日中值式子相除.
凑巧两个的 是同一个

Q: 什么情况下适合使用柯西中值定理呢?
A: 有条件为参数方程
正好有 ,

参数方程也会有特点. 一般一个具体, 一个抽象, 正适合考研的难度
具体可见例 6.11

Q: 带拉格朗日余项的 阶泰勒公式
A: 设 在点 的某个邻域内 阶导数存在, 则对该邻域内的任意点 , 有

Q: 带佩亚诺余项的 阶泰勒公式
A: 设 在点 处 阶可导, 则存在 的一个邻域, 对于该邻域内的任意点 , 有局部上

Q: 拉格朗日型余项泰勒公式与佩亚诺型余项泰勒公式的条件与结论的不同
A: 拉格朗日型余项泰勒公式: 要求函数在一个区间上 阶可导. 它给出了在任意偏离点 的点 处, 余项的一个精确表达式的结论.
佩亚诺型余项泰勒公式: 只要求函数在一个点 处 阶可导. 它描述了当 无限趋近于 时, 余项的数量级

Q: 拉格朗日余项与佩亚诺余项泰勒公式谁的条件更强
A: 拉格朗日条件更强. 要求邻域内都可导

Q: 泰勒公式的数学意义 ( 与 的关系)
A: 已知 可以估计出附近邻域或区间内的其他 的值.
以近似替换的手段实现函数值的估计

当{}时, 被称作麦克劳林公式, 余项为{拉格朗日与佩亚诺都可以}

您好! 您的描述在核心思想上是基本正确的, 抓住了两者最关键的区别. 但是, 其中一些表述 (特别是”超实数邻域”) 不够精确, 可能会引起误解.

我们来更准确、更系统地梳理一下拉格朗日型余项泰勒公式和佩亚诺型余项泰勒公式的区别.

关系图谱