数制转换
将十进制转换为任意进制数
基数乘除法
对整数部分采用{c1: 除基取余}法
先余为{c2: 低}, 后余为{c2: 高}
算到整数部分为 0 为止
对小数部分采用{c3: 乘基取整}法
先整为{c4: 高}, 后整为{c4: 低}
算到小数部分为 0 为止
Q: 任意一个十进制小数都可以用二进制小数表示吗?
A: 不行
任何十进制的小数都可以用二进制表示
但不是所有的二进制小数都可以用十进制表示
真值与机器数
真值与机器数的比较
真值是{实际的数值}, 例如-1,+3…
机器数是{c2: 真值}在{c2: 机器}中的表示
有多种不同的表示方法
- 原码
- 补码
- 反码
- 移码
不论真值为正数还是负数
补码的{补码}是{原码}
真值与原码
真值为
If (x>=0)
原码={c1:0. X}
If (x<0)
原码={c1:1. X}
真值与反码
真值为
If (x>=0)
反码={c1:0. X}
If (x<0)
反码={c1:1.
真值与补码
真值为
If (x>=0)
补码={c1:0. X}
If (x<0)
补码={c1:1.
真值与移码
真值为
在真值的基础上加上一个偏置
若 x 长度为
一般偏置为{
真值为 0
{原码, 反码}, 表示不唯一
{补码, 移码}, 表示唯一
Q: 如何从
A:
Ｃ语言中的整数类型及类型转换
计算机中
有符号整型数据都是按{c1: 补码}形式储存
无符号整型数据都是按{c1: 二进制编码}形式储存
Q: 等长的整数有符号变量与无符号变量强制转换
A: 只是改变了第一位的解释
有符号数解释为符号位
无符号数解释为最高数值位
整数有符号变量与无符号变量参与运算, 则 C 语言标准规定按{无符号}变量进行运算
Q: 在 C 语言中, int 类型变量与 short 类型变量相加, 结果为什么类型变量?
A: int 类型
Q: 整数无符号大字长变量向小字长变量强制转换
A: 所有的无符号整数都直接用二进制保存
高位截断, 低位不变
Q: 整数有符号大字长变量向小字长变量强制转换
A: 所有的有符号整数都用补码的形式保存
不考虑原来的符号位, 直接高位截断, 低位不变
结果的最高位就当作类型转换之后的符号位. 该结果也是对应真值的补码表示
Q: 整数小字长变量向大字长变量强制转换
A: 低位不变, 高位拓展
若原数字是无符号整数, 则进行零扩展
若原数字是有符号整数, 则进行符号扩展
各种类型变量的长度
标志位的意义与判断
四大标志位的英文与意义
OF {Overflow Flag}
ZF {Zero Flag}
CF {Carry Flag}
SF {Sign Flag}
定点数的移位运算
逻辑移位和算术移位的区别
逻辑移位将所有的操作数都视作无符号数
算术移位将所有的操作数都视作有符号数
移位的补全
逻辑移位
- 左移: 低位补 0
- 右移: 高位补 0
算数移位 - 左移: 低位补 0
- 右移: 高位补符号位
移位的溢出判断
不管是逻辑移位还是算术移位
只有{左移}会发生溢出
逻辑移位:{高位 1 移出}, 则溢出
算术移位:{左移前后符号位不同}, 则溢出
定点数的加减运算
OF 的判断
不管是有符号还是无符号数, 通通当作有符号
- 从计算机角度
双符号位
{ }
符号位进位为, 最高数值位进位为
{ } - 从人角度
CF 的判断
不管是有符号还是无符号数, 通通当作无符号
- 使用
判断
{ } - 从人角度
Q: 什么是模四补码?
A: 一种变形补码
用两个二进制位来表示数字的符号位, 其余与补码相同
Q: 模 4 补码储存的时候需要几个符号位?
A: 储存的时候只用一个符号位
这是因为任何一个正确的数值, 模 4 补码的两个符位总是相同的
但在 ALU 中, 运算的时候, 是双符号位
符号位向高位拓展一次
定点数的乘除运算
乘法
Q: 原码定点数
定点数原码乘法运算
A: 1. 符号位:
2. 数值位:
画图, 32 位无符号数乘法运算的逻辑电路图
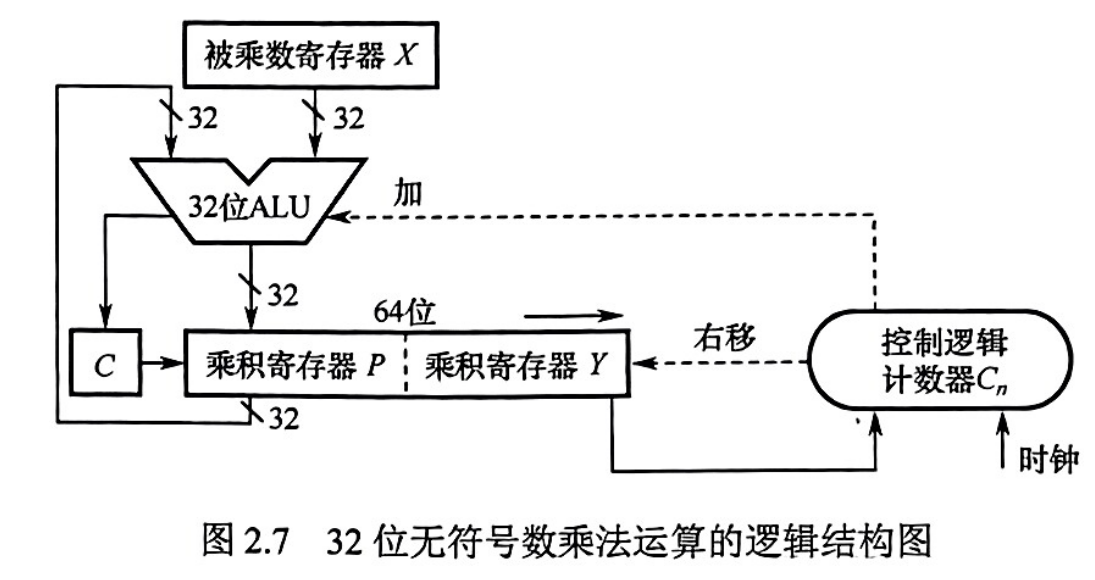
32 位乘法运算的溢出判断
有符号 (int)
不溢出条件: {c1:64 位乘积的高 32 位, 等于低 32 位符号位的扩展}
溢出条件: {c1:64 位乘积的高 32 位, 不等于低 32 位符号位的扩展}
无符号 (unsigned int)
不溢出条件: {c2:64 位乘积的高 32 位全部为 0}
溢出条件: {c2:64 位乘积的高 32 位不全为 0}
除法
Q: 原码定点数
定点数原码除法
A: 1. 符号位:
2. 拓展: 被除数
3. 数值位:
画图, 32 位无符号数除法运算的逻辑电路图
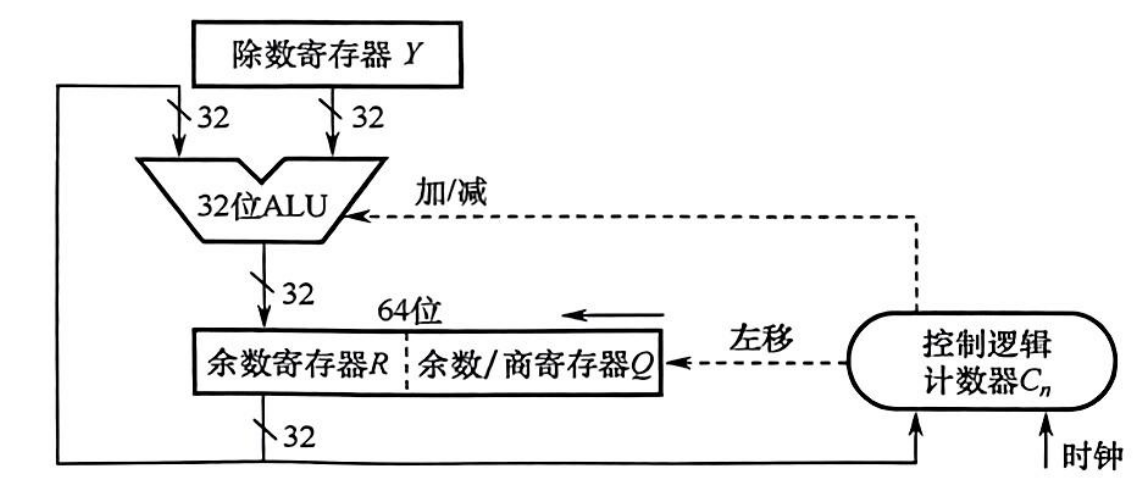
浮点数的表示与规格化
浮点数的表示
符号
阶码: 通常用补码, 移码表示
尾数: 通常用补码, 原码表示
浮点数的规格化
左规:
最高有效位为 0. 做左规可能出现多次
右规: 小数点左边存在有效位. 右规只有一次, 有可能导致上溢
IEEE754
IEEE754 标准的浮点数格式
- 位数
单精度:
符号{c1:1}阶码{c1:8}尾数{c1:23}
双精度:
符号{c2:1}阶码{c2:11}尾数{c2:52} - 机器数表示
阶数用{c3: 移码}表示, 偏置为 {c3:}
单精度偏置:127
双精度偏置:1023
尾数用{c3: 原码}表示 - 隐藏有效位
在尾数左边隐藏了一个有效位 1
IEEE754 标准的浮点数格式
阶数的取值范围
单精度:{c1:[-126,127]}
双精度:{c1:[-1022,1023]}
IEEE754 标准的浮点数 Floating-point=S,E,m
S 为符号位, E 为阶数位, m 为尾数位
真值计算公式:{
注意阶数位
IEEE 特殊表示需要记住吗
浮点数的加减运算
Q: 浮点数的加减运算公式化做题五步走
A: - 对阶
- 尾数运算
- 尾数规格化
- 舍入
- 溢出判断
尾数用原码表示, 规格化
目标为最高数值位=1
左规, 末位补 0
右规, 高位 0
尾数用补码表示, 规格化
目标为符号位
左规, 末位补 0
右规, 高位补符号位