图的基本概念
图的数学定义是什么?
图
Q: 无向图的边和有向图的弧有什么区别?
A: 无向图的边是顶点的无序对, 而有向图的弧是顶点的有序对.
Q: 边的数量符合什么条件为完全图?
A: 无向图: 有
有向图: 有
Q: 完全图一定是连通图吗?
A: 是的, 根据完全图的定义, 任意两个顶点之间都存在边, 所以它必然是连通的.
Q: 有图为
子图的定义
A: 有图为
若
则
Q: 有图为
生成子图的定义
A: 在子图的基础上再加一个条件
Q: V 和 E 的任何子集都能构成 G 的子图吗?
A: 错误
显然, 如果任意取
而在
图的定义不满足
图可以有度为 0 的点, 但不能有边/弧连接不存在的点
连通与强连通都是描述图连通的特性, 但是描述的对象不同
连通用来描述{c1: 无向图}
强连通用来描述{c1: 有向图}
Q: 极大连通子图的定义
A: 包含图中尽可能多的顶点以及尽可能多的边, 并且连通
Q: 连通分量与极大连通子图的关系
分为两种情况, 1. 图本身为连通图 2. 图本身为非连通图
A: 连通图: 连通分量=极大联通子图=连通图本身
非连通图: 连通分量=多个极大联通子图
Q: 什么是图的最大连通分量?
A: 在一个非连通图中, 包含顶点数最多的那个连通分量被称为最大连通分量.
Q: 生成树去掉一条边/添加一条边会发生什么?
A: 去掉一条边: 极小连通子图变为不连通
添加一条边: 出现一个回路
Q: n 个顶点的非连通图, 最多多少条边?
A: 由
总数为
Q: 有 n 个顶点
最少多少边能构成一个无向连通图
A: 边最少的无向连通图为生成树/极小连通子图
最少要 n-1 条边
Q: 有 n 个顶点
最少多少边能构成一个有向连通图
A: 边最少的有向连通图为环
最少要 n 条边
Q: 连通图有唯一的极小连通子图吗?
A: 有多个不同的极小连通子图
Q: 什么样的图才能有极小连通子图呢?
A: 连通图
极小连通子图仅仅在连通图中有意义
Q: 极小连通子图的定义
A: 包含图的所有点, 且相互连通, 边最少, 不存在回路
若图有
Q: 怎样的图能够获得生成树?
A: 连通图
Q: 怎样的图能够获得生成森林?
A: 非连通图
Q: 如何从连通图中获取生成树?
A: 取连通图中的极小连通子图
(生成树与极小连通子图等价)
Q: 如何从非连通图中获取生成森林
A: 取其中的连通分量 (全部极大连通子图)
连通分量 (每个极大连通子图) 的生成树 (极小连通子图) 组成了连通森林
Q: 生成树与生成森林的关系
A: 多个生成树组成一个生成森林
Q: 对于一个连通图, 从任意顶点出发进行一次深度优先搜索 (DFS) 可以访问到所有顶点吗?
A: 可以.
有向图中
出度+入度={(总) 度}
图的储存及基本操作
Q: 在图的存储结构中, 哪些表示方法是唯一的, 哪些是不唯一的?
A: 邻接矩阵的表示是唯一的; 邻接表、十字链表和邻接多重表的表示是不唯一的.
设图 G 的邻接矩阵为
邻接表法、十字链表和邻接多重表的共同存储特点是: 顶点结点之间采用{顺序存储}, 边结点之间采用{链式存储}.
图的遍历
什么样的路径序列被叫作简单路径?
顶点不重复出现的路径称为简单路径
什么是图的简单回路?
除了第一个顶点和最后一个顶点相同外, 其余顶点不重复出现的回路称为简单回路.
简单路径中是否包含回路?
不包含.
BFS, DFS 与树的遍历
广度优先搜索的过程与树的{层次遍历}类似
深度优先搜索的过程与树的{先序遍历}类似
BFS/DFS 在使用邻接矩阵时的时间复杂度为{
BFS与DFS的时间复杂度
图的存储结构
邻接矩阵:{
邻接表:{
BFS/DFS 的空间复杂度为{c1:
Q: 非带权图的单源最短路径问题使用 BFS 还是 DFS?
A: BFS
对同样一个图,
基于邻接矩阵的遍历得到的 DFS 序列和 BFS 序列{c1: 是}唯一的,
基于邻接表的遍历得到的 DFS 序列和 BFS 序列{c1: 不是}唯一的.
BFS 需要调用空间复杂度为{c1:
DFS 需要调用空间复杂度为{c2:
Q: 除了拓扑排序, 还有什么遍历算法可以用来判断有向图是否存在环?
A: 深度优先遍历 (DFS) 算法.
Q: 图的广度优先生成树的树高与深度优先生成树的树高比较
A: 图的广度优先生成树的树高⇐深度优先生成树的树高
图的应用
最小生成树算法
Q: 什么是最小生成树 (MST)?
A: 对于一个带权连通无向图, 其所有生成树中, 边的权值之和最小的那棵生成树就是最小生成树.
Q: Prim 算法的核心操作是什么?
A: 从一个顶点开始, 不断选择代价最小的边来扩展生成树.
Q: Kruskal 算法的核心操作是什么?
A: 从边出发, 不断加入权值最小且不会构成回路的边
Q: Prim 算法与 Kruskal 算法的主要区别是什么?
A: Prim 算法从点开始得到生成树
Krusal 算法从边开始得到生成树
图中没有权值相同的边是最小生成树唯一的{充分不必要}条件
图最小生成树 (MST) 唯一的判定流程
- 使用 kruskal 算法得到生成树 MST
- 将图中任意一条不属于 MST 的边 e 加入 MST, 得到一个回路 C
- 判断 e 是否是大于回路 C 中其他边的权值
Q: Prim 算法与 Kruskal 算法分别适用于什么类型的图?
A: Prim: 边稠密
Kruskal: 边稀疏
对于不同的图存储结构, Prim 和 Kruskal 算法的时间复杂度分别是多少?
- Prim 算法
邻接矩阵:
邻接表: - Kruskal 算法
邻接矩阵:
邻接表:
Q: 最小生成树算法有哪些?
A: Prim
Kruskal
最短路径算法
图论中的最短路径算法主要有哪些?
{BFS} 算法
{Dijkstra} 算法
{Floyd} 算法
最短路径算法的适用范围
BFS 算法: {无权图的单源}最短路径
Dijkstra 算法: {无负权值图的单源}最短路径
Floyd 算法: {每对顶点间的}最短路径, 可以处理负权值但不能处理负权回路.
Q: 哪个最短路径算法可以得到多个顶点之间的最短路径?
A: Floyd 算法
Q: Dijkstra 算法的核心思想是什么?
A: 每次找出到源点距离最近且未被访问过的顶点, 将其归入已确定最短路径的集合, 并用这个点去更新源点到其他所有未访问顶点的距离.
Q: 画出 a 到各个顶点最短路径的求解过程
使用 Dijkstra 算法
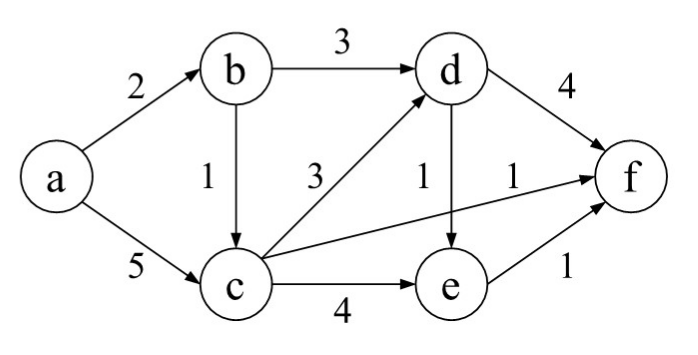
A: 
Dijkstra 算法的时间复杂度是多少?
时间复杂度为
Dijkstra 算法的时间复杂度受图的存储结构影响吗?
不受邻接矩阵或邻接表存储结构的影响
Q: Floyd 算法的核心思想是什么?
A: Floyd 算法通过动态规划思想, 每次尝试引入一个新顶点作为中间点, 来更新图中任意两点间的最短路径.
Q: Floyd 算法的时间复杂度是多少?
A:
Q: BFS 算法可以用来求解哪种图的单源最短路径问题?
A: 无权图 (或所有边权值相同的图).
Q: 什么是 DAG 图?
A: 有向图中不存在环
拓扑排序的时间复杂度与图的存储结构
邻接表存储:{
邻接矩阵存储:{
Q: 对图进行深度优先遍历 (DFS) 可以得到拓扑排序吗?
A: 可以.
Q: 在什么情况下, 一个图的拓扑排序结果通常不唯一?
A: 当图中某个顶点有多个直接后继时, 拓扑排序的结果通常不唯一.
Q: 在什么情况下, 一个图的拓扑排序结果是唯一的?
A: 当图中每个顶点都有唯一的前驱和后继关系时, 拓扑排序的结果是唯一的.
Q: AOV 网和 AOE 网的主要区别是什么?
A: AOV (Activity on Vertex) 网中的边没有权值, 主要表示活动间的优先关系; AOE (Activity on Edge) 网中的边有权值, 通常表示活动持续的时间.
在 AOE 网中, 关键活动是指{e=l}的活动, 其中 e 是活动的最早开始时间, l 是活动的最晚开始时间.
Q: 什么是关键路径? (时间定义与长度定义)
A: 长度定义: 从源点到汇点路径长度最长的路径.
时间定义: 最早发生时间与最晚发生时间相同
Q: 在 AOE 网中, 如何计算各个事件的最早发生时间 (ve) 和最晚发生时间 (vl)?
A: - 求 ve: 从源点开始进行拓扑排序, ve (j) = max{ve (i) + weight (i, j)}, 其中 (i, j) 是以 j 为终点的所有活动.
- 求 vl: 从汇点开始进行逆拓扑排序,
vl (i) = min{vl (j) - weight (i, j)}, 其中 (i, j) 是以 i 为起点的所有活动.
Q: 在一个带权图的最小生成树中, 某条边的权值是否可能超过未被选中的边的权值?
A: 可能. 最小生成树保证的是总权值最小, 而不是选择的每一条边都是局部最小的.
使用 DFS 算法遍历有向无环图 (DAG) 时, 如何得到拓扑有序和逆拓扑有序序列?
A: - 递归结束前输出顶点信息: 得到逆拓扑有序序列.
- 递归结束后输出顶点信息: 得到拓扑有序序列.
Q: 在无向连通图中, 如果没有权值相同的边, 它的最小生成树是否唯一?
A: 是, 唯一.
判断一个有向图是否有环的常用方法有哪些?
{深度优先遍历 (DFS)}
{拓扑排序}
有向图中入度为 0 和出度为 0 的顶点都仅有 1 个是拓扑有序序列唯一的{充分不必要条件}
Q: 如何缩短一个工程的关键路径? (一条和多条)
A: - 如果只有一条关键路径, 缩短该路径的长度.
- 如果有多条关键路径, 必须同时缩短每一条关键路径的长度.