树
树的定义是递归的, 即在树的定义中又用到了其自身, 树是一种递归的数据结构.
树作为一种逻辑结构, 同时也是一种分层结构
因为树中的分支是有向的, 即从双亲指向孩子, 所以树中的路径是从上向下的
Q: 树中结点数与度数之和的公式是什么?
A: n=所有度数之和+1
度为m的树中第 i 层上至多有{
二叉树
Q: 二叉树的定义:
A: 每个结点至多有两棵子树 (度为 2)
Q: 二叉树可以没有度为 2 的结点吗?
A: 可以, 二叉树的定义: 每个结点至多只有两棵子树 (度为 2)
没有度为 2 的结点, 依然可以是一个二叉树
Q: 二叉树可以为空吗?
A: 可以, 二叉树是 n (n≥0) 个结点的有限集合
当 n=0 时候
二叉树为空二叉树
二叉树与度为 2 的有序树有哪些不同的地方 (空二叉树, 有序性)
①度为 2 的树至少有 3 个结点, 而二叉树可以为空.
②度为 2 的有序树的孩子的左右次序是相对于另一个孩子而言, 一个度为 1 的结点, 其叶子结点不论在左边还是右边, 都没有区别
而二叉树的左右次序是相对于根结点而言, 一个度为 1 的结点, 其叶子结点在左边还是在右边是不同的
满二叉树: 二叉树中的每层都含有最多的结点
完全二叉树: 类似于满二叉树, 但是不保证每一层都拥有最多的结点
二叉排序树: 也是递归定义的左子树上所有结点的关键字均小于根结点的关键字; 右子树上所有结点的关键字均大于根结点的关键字; 左子树和右子树又各是一棵二叉排序树
平衡二叉树: 树中任意一个结点的左子树和右子树的高度之差的绝对值不超过 1
正则二叉树: 树中每个分支结点都有 2 个孩子, 即树中只有度为 0 或 2 的结点
Q: 非空二叉树上的叶结点数与度为 2 的结点数的关系
A:
Q: 二叉排序树是平衡二叉树吗?
二叉搜索树呢?
A: 二叉排序:不是
二叉搜索:是
Q: 平衡二叉树的组建过程
依次将1,2,3,4,5,6,7插入初始为空的平衡二叉树中,画出过程
A: 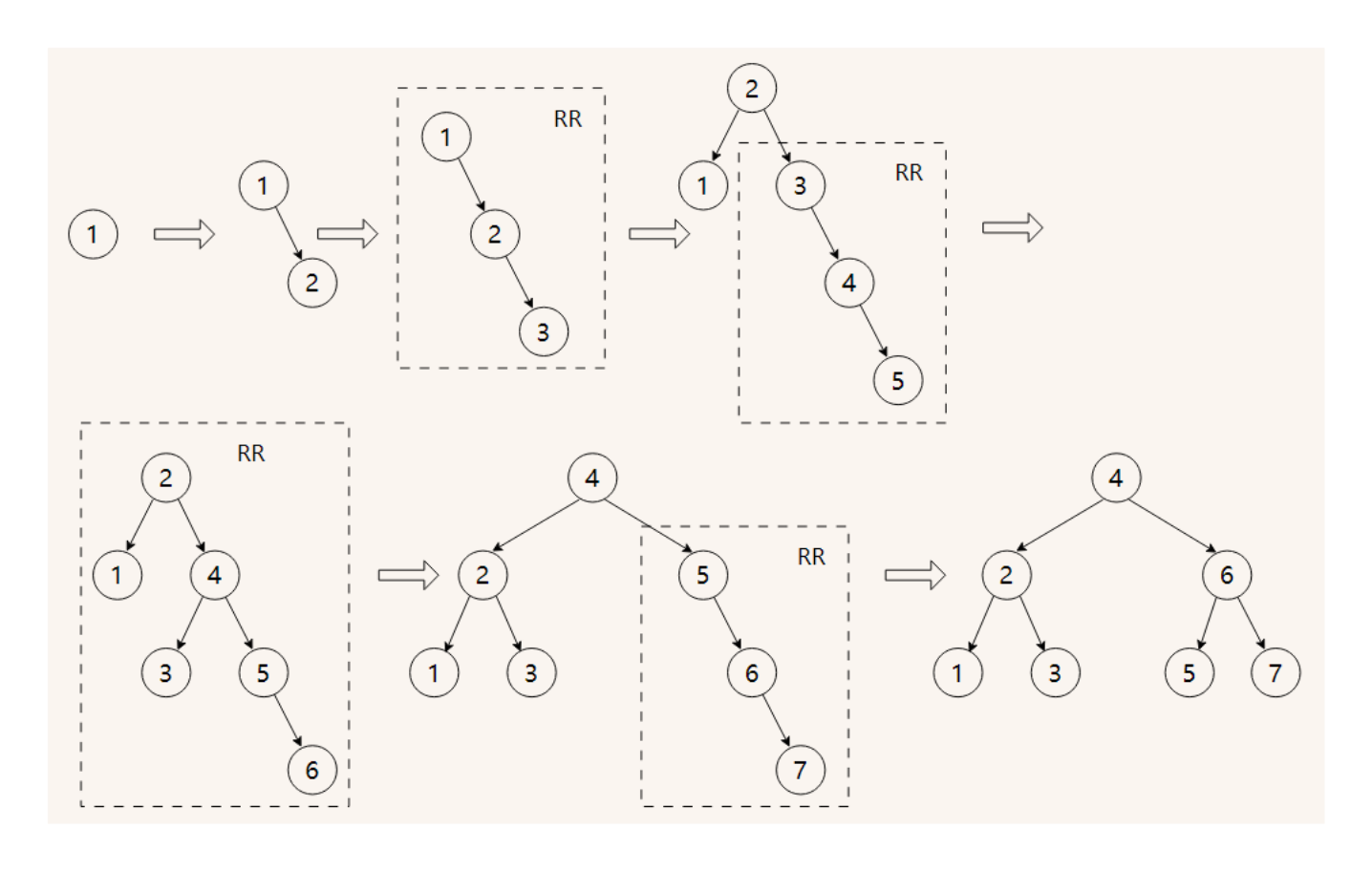
Q: 平衡二叉树深度为 h, 最少结点数为?
A:
平衡二叉树深度为 h
{最少结点数为?}
⇐>
{所有结点的平衡因子均为1,则结点数为?}
具有 n 个 (n>0) 结点的完全二叉树的高度为{
二叉树的存储
顺序存储:
完全二叉树, 满二叉树
链式存储 (二叉链表):
一般二叉树
含有 n 个结点的二叉树中, 含有 {
Q: “二叉树为空”意味着二叉树不存在吗?
A: 错误
二叉树的结点数
二叉树的遍历
先序遍历和中序遍历的算法实现是类似的
后序遍历的算法实现则不同
非递归的后序遍历 (使用栈数据结构) 的作用
根到某结点的路径, 求两个结点的最近公共祖先
删除该二叉链表中的所有结点, 并释放它们占用的存储空间
非递归的后序遍历, 栈的情况
Q: 确定唯一的二叉树, 需要哪些遍历的结果?
A: 中序加上其他某种 (先序, 后序, 层次) 遍历确定唯一对应的二叉树
Q: 如果只有先序遍历和后序遍历能够确定什么?
A: 不能够确定唯一的二叉树, 但可以确定二叉树中结点的祖先关系
当先序为
线索二叉树
Q: 线索二叉树是如何在二叉链表基础上进行改良的?
A: 利用了多余的
再加上两个标志位 ltag 与 rtag
If *tag=0
*child 指向孩子
Else if *tag=1
*child 指向前驱/后继
*代表 l 或者 r
二叉树的线索化是将二叉链表改为线索二叉树
空指针改为指向前驱或者后继的指针
因此线索化的实质就是遍历一次二叉树后, 更新二叉链表
Q: 不同的遍历顺序 (前序中序后序) 对应的线索二叉树相同吗?
A: 不同的遍历顺序对应不同的线索二叉树
Q: 带头结点的线索二叉树与不带头结点的线索二叉树有什么不同点?
A: 第一个结点的 lchild 指针指向头结点
最后一个结点的 rchild 指针指向头结点
Q: 二叉树的不同遍历寻列中, 叶结点的先后顺序相同吗?
A: 完全相同, 不同的遍历顺序影响的只有根节点于遍历序列中的位置. 不影响叶子结点的顺序
Q: 对二叉链表线索化后, 链表 (二叉树) 中空指针的个数
A: 不能够确定
具体情况具体分析
不同的树, 不同的线索化方法, 空指针的数量不同
后序线索树的遍历仍需要栈的支持
Q: 已知先序中有
A:
由先序和中序, 能够确定唯一的二叉树可知, 求可能的二叉树的个数, 就是求可能的中序的个数
从栈的角度来考虑先序与中序
先序等于告诉入栈的顺序
而中序为出栈的顺序
由栈的知识点可知
当有
所以已知先序中有
已知中序中有
具体问题具体分析
已知中序, 来倒推先序
中序等于告诉出栈的顺序
而先序为入栈的顺序
就是已知出栈顺序, 倒推进栈顺序
但是没有一个简单的公式可以直接计算所有情况, 但可以通过递归或动态规划的方法针对具体序列进行计算. 对于较小的 n, 可以手动枚举并验证
树, 森林
树的双亲表示法
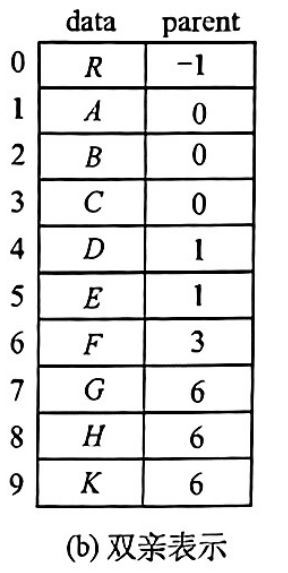
顺序存储结构
优点: 可以很快地得到每个结点的双亲结点
缺点: 求结点的孩子时则需要遍历整个结构
Q: 树的双亲表示法是什么存储结构?
A: 顺序存储
Q: 使用树的双亲表示法存储这棵树
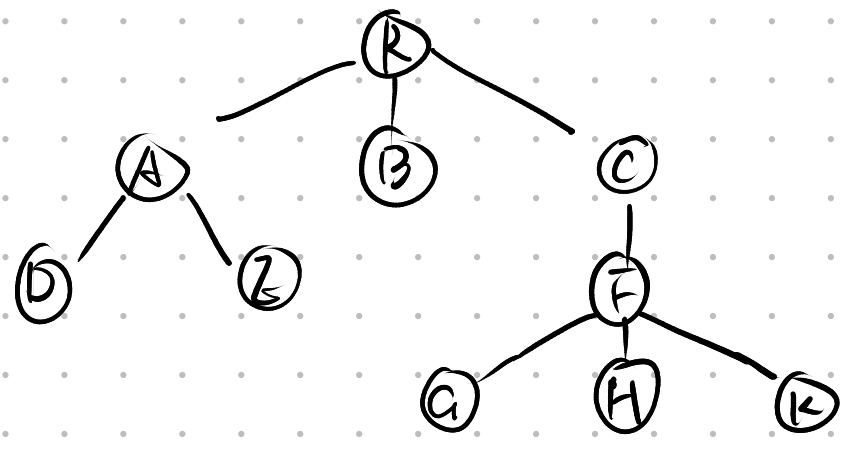
A: 
孩子表示法
链式存储结构与顺序存储结构的复合
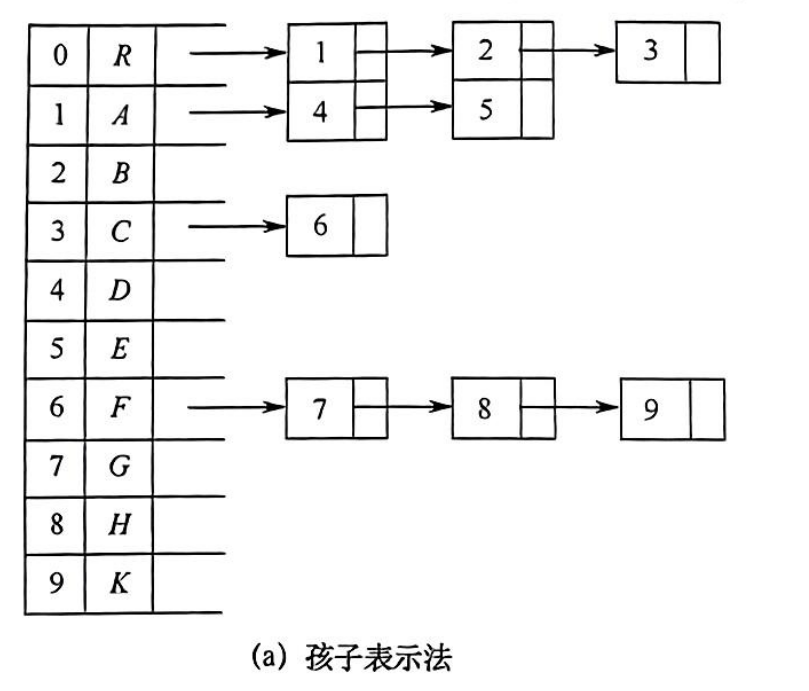
蓝色部分是顺序存储
绿色部分是链式存储
与双亲表示法相反
优点: 可以很快地得到每个结点的孩子结点
缺点: 求结点的双亲时则需要遍历整个结构
Q: 树的孩子表示法是什么存储结构?
A: 顺序与链式复合的存储结构
Q: 使用树的孩子表示法存储这棵树
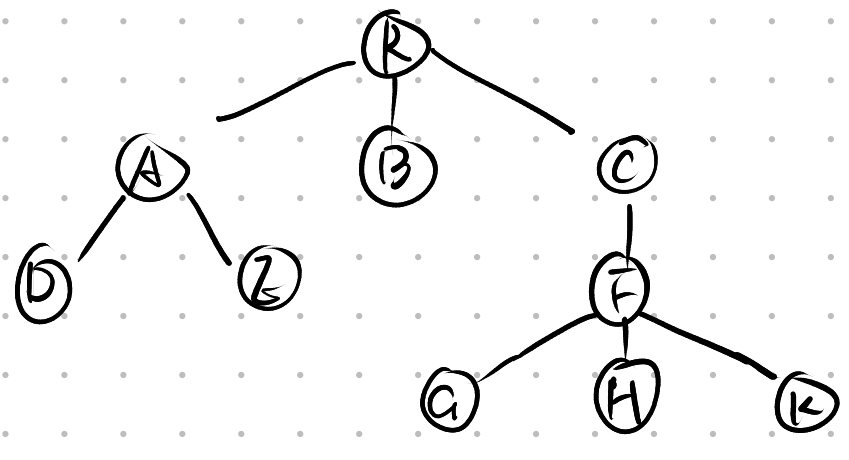
A: 
孩子兄弟表示法:
将树转化为二叉链表表示
结点为左孩子右兄弟, 中间自身的数据
优点: 是可以方便地实现树转换为二叉树的操作, 易于查找结点的孩子等
缺点: 从当前结点查找其双亲结点比较麻烦. 若为每个结点增设一个 parent 域指向其父结点, 则查找结点的父结点也很方便.
Q: 如何使用孩子兄弟表示法将树转化为二叉树
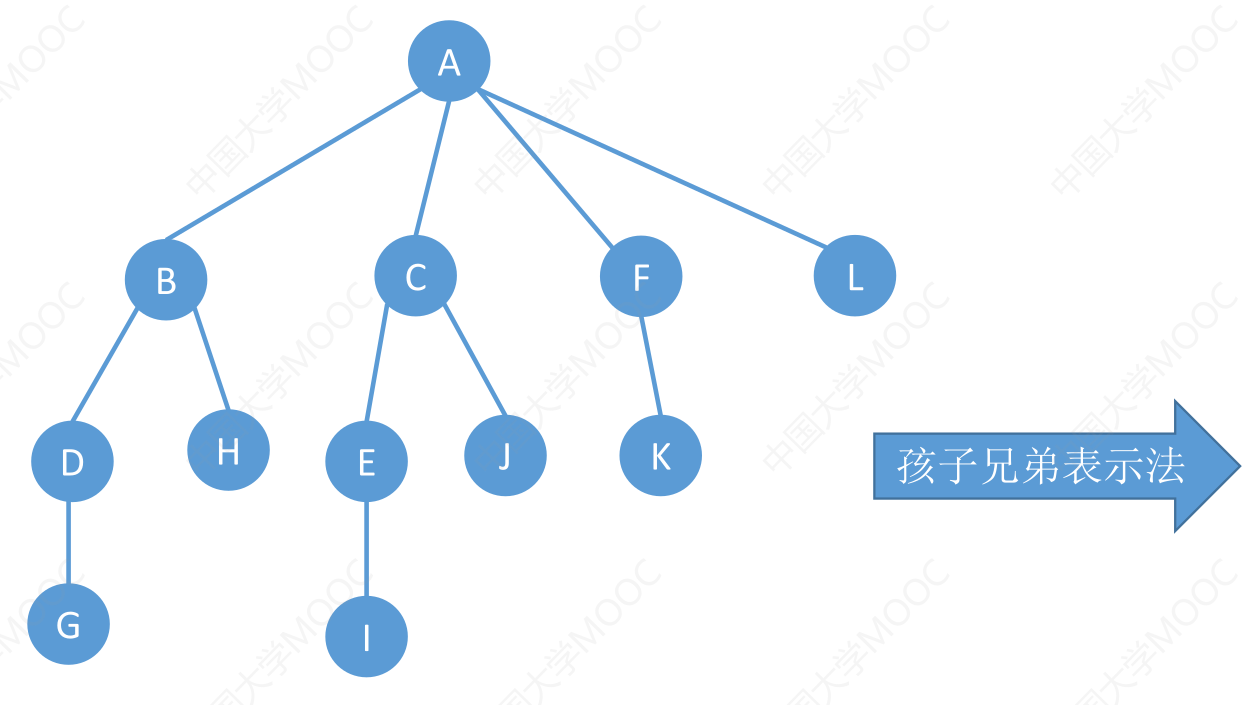
A: 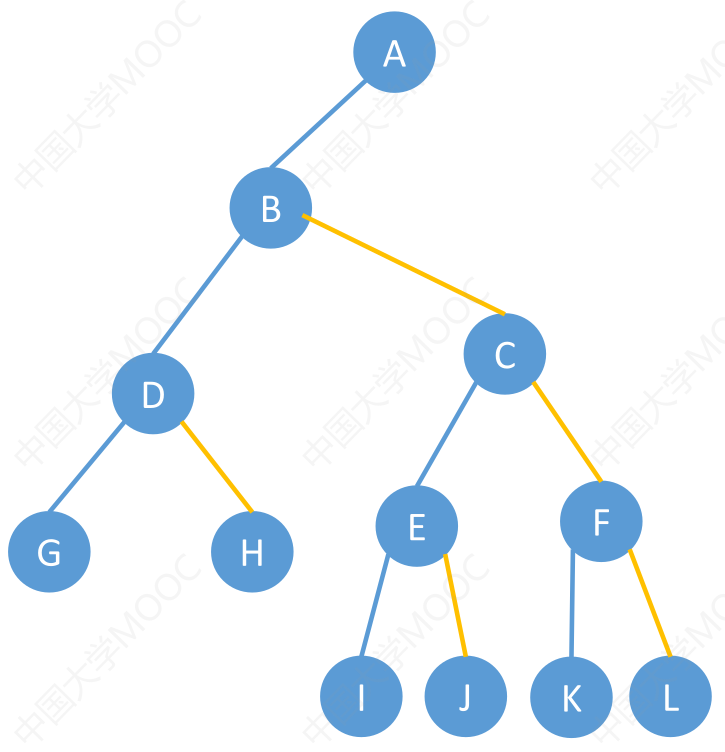
①先在二叉树中, 画一个根节点.
②按”树的层序”依次处理每个结点.
处理一个结点的方法是: 如果当前处理的结点在树中有孩子, 就把所有孩子结点
“用右指针串成糖葫芦”, 并在二叉树中把第一个孩子挂在当前结点的左指针下方
使用兄弟孩子表示法,将树A转化为二叉树B,
A中{分支结点数+1}=B中{无右孩子结点数}
使用兄弟孩子表示法,将森林A转化为二叉树B
A中叶节点数=B中无左孩子结点数
Q: 如何使用孩子兄弟表示法将森林转化为二叉树
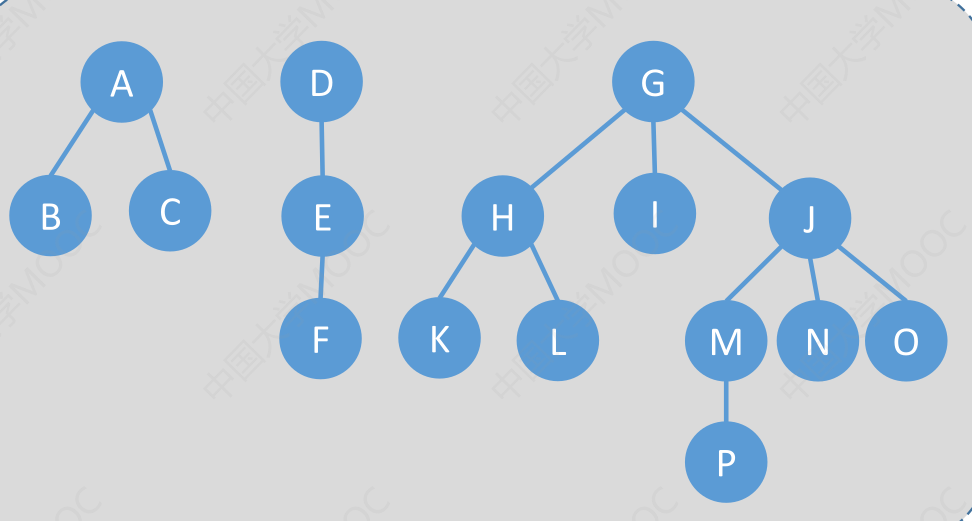
A: 与将树转化为二叉树方法类似
先把所有树的根结点画出来, 在二叉树中用右指针串成糖葫芦
按”森林的层序”依次处理每个结点
处理一个结点的方法是: 如果当前处理的结点在树中有孩子, 就把所有孩子结点
“用右指针串成糖葫芦”, 并在二叉树中把第一个孩子挂在当前结点的左指针下方
二叉树 (BT), 树 (T), 森林 (F) 的相互转化
二叉树转换为树或森林是唯一的
树/森林的先根遍历 (先序遍历)=其相应二叉树的先序序列
树/森林的后根遍历 (后序遍历)=其相应二叉树的中序序列
森林与二叉树的对应关系
BT 是由 F 变换来的二叉树
F 中叶结点的个数等于 BT 中左孩子指针为空的结点个数
F 中非叶节点的个数等于 BT 中右指针为空的结点个数+1
树与二叉树的应用
Q: 什么是哈夫曼树?
A: 最小带权路径长度的二叉树, 又称最优二叉树
Q: 什么是最小带权路径长度?
A: 从根节点到所有叶子结点, 带权路径总和最低
n 是叶子节点的数量
在构造 K 叉哈夫曼树时,有一个前提条件:(n - 1) 必须是 (K - 1) 的整数倍
哈夫曼树的最关键的特点
不存在度为{1}的结点
哈夫曼树也被叫作{最佳归并}树
前缀编码的定义:
没有一个编码是另一个编码的前缀
哈夫曼编码
使用哈夫曼树生成的前缀编码
总长度最短的二进制前缀编码
效率最高的前缀编码
并查集
并查集的存储结构
顺序存储
树的双亲数组表示法
并查集的优化
Union 操作优化
将小树合并为大树
深度不超过
时间复杂度为
Find 操作优化
压缩路径
将路径上元素的直接指向树根
时间复杂度为
并查集的作用: