🪴 l4rk's Quartz

18多元函数微分学

17分钟阅读

三重积分

三重积分的计算
直角坐标系
先 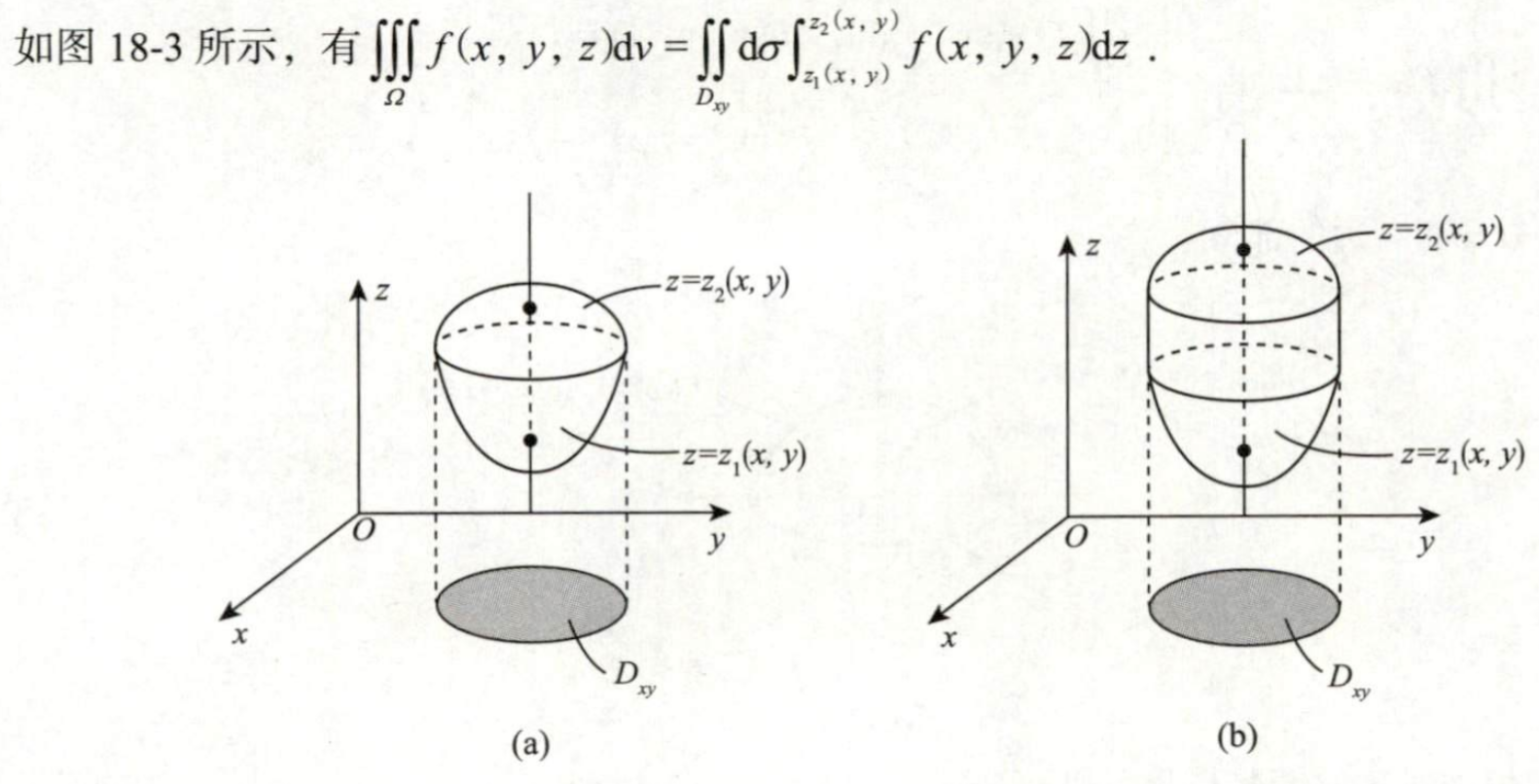后 (投影穿线法) 一般用在积分空间侧面为{柱面}或者{无侧面}

三重积分的计算
直角坐标系
先 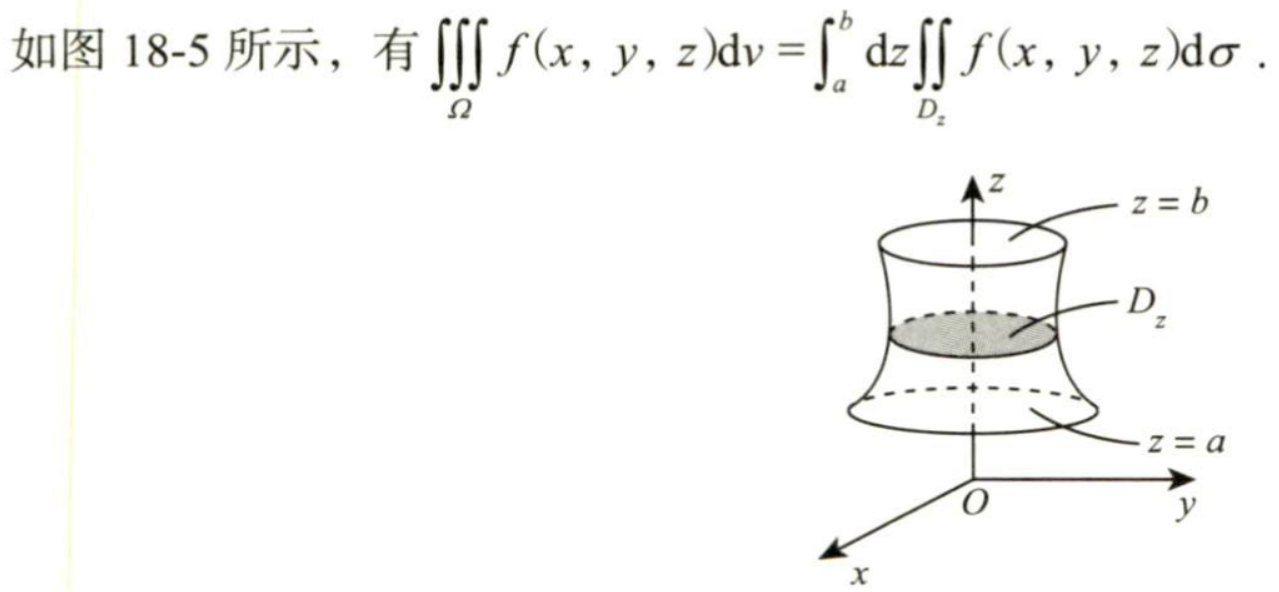后 (定限截面法) 一般用在积分空间是{旋转体}

三重积分的计算
柱面坐标系在直角坐标系的计算中
,如若 适用于极坐标系, 则令{}便有 {}

三重积分的计算
球面坐标系
什么时候适合使用球面坐标系?
a.被积函数中含{}
b.积分区域为{球或球的部分锥或锥的部分}

三重积分的计算
球面坐标系
{}

三重积分换元中的雅克比行列式是用来刻画同一个积分空间在不同坐标系下的测度变化的{倍数}
在新的坐标系中, 乘上雅克比行列式的绝对值, 保证新坐标系的测度值与原坐标系相同

Q: 雅克比行列式的换元
将 换元为
令 , 计算
A:

换元法具体形式

物理应用

Q: 对于空间物体, 若体密度为 是物体所占的空间区域, 则计算重心 (形心)( 的公式为
A:


注意形心公式的逆用

Q: 对于空间物体, 若体密度为 是物体所占的空间区域, 则计算该物体对 轴、 轴、
轴和原点 的转动惯量 和 公式分别为
A:

Q: 对于空间物体, 若体密度为 是物体所占的空间区域, 则计算该物体对物体外一点
处的质量为 的质点的引力 公式为 (总与各个方向)
A:


第一类曲线积分

第一类曲线积分是由定积分推导过来

平面曲线

第一类曲线积分, 显式方程
若平面曲线 由 给出
{c1: }
{c1: }

第一类曲线积分, 参数方程
若平面曲线 由 , , 给出
{c1: }
{c1: }

第一类曲线积分, 极坐标方程
若平面曲线 由极坐标形式 给出
{c1: }
{c1: }
值得注意, 极坐标式 与别的不太一样

空间曲线

若空间曲线由参数式 , 给出
{c1: }
{c1: }

物理应用

Q: 对于空间光滑曲线 ,若线密度为 , 则计算重心 (质心) 的公式为
A:
注意逆用

Q: 对于空间光滑曲线 , 若其由参数式 , 给出, 则计算空间曲线的长度 (弧长) 的公式为
A:

Q: 对于光滑曲线 ,线密度为 , 则计算该曲线对 轴、 轴、 轴和原点 的转动惯量 和 公式分别为
A:

第一类曲面积分

为面 的外法向量方向余弦
则 ={c1: }
={c1: }
={c1: }

第一类曲面积分计算的基本方法:
将第一类曲面积分化为 {二重积分}
一投二代三计算

曲面由 确定
投影至 面, 计算曲面面积
{}

Q: 第一类曲面积分的过程
A: 投影, 化为二重积分计算

Q: 对于光滑曲面薄片 , 若面密度为 , 则计算重心 的公式为
A:

Q: 对于光滑曲面薄片 , 若面密度为 , 则计算该薄片对 轴、 轴、 轴和原点 的转动惯量 和 的公式分别为
A:

第二类曲线积分

平面曲线

第二类曲线积分转化为第一类曲线积分
{}
为切向量与 轴的夹角
为切向量与 轴的夹角

平面第二类曲线积分的计算
基本方法化为定积分

  • 参数方程
    由参数方程 给出, 则
    {}
  • 一般方程
    由方程 给出, 可以看作参数方程 于是有
    {}

第二类曲线积分的计算方法

  1. 参数法
  2. 降维法
  3. 格林公式 (平面曲线)
  4. 斯托克斯公式 (空间曲线)

Green 公式

平面第二类曲线积分的计算
格林公式
{}

Q: 平面第二类曲线积分使用格林公式的三大条件
A: - 围成的是有界闭区域

  • 方向为正向
  • 在 上 有一阶连续偏导

平面第二类曲线积分使用格林公式
三种应用情况

  • 曲线封闭并且{没有奇点在内部} 直接使用 green 公式
  • 非封闭曲线且{} 可补线使其封闭 (加线减线)
  • 曲线封闭但有奇点在其内部, 且除奇点外, 其他点都满足{} 换路径

平面第二类曲线积分的计算
格林公式
曲线封闭但有奇点在其内部, 且除奇点外 换路径的本质

将一个不能用 green 公式计算的第二类平面积分, 使用积分路径无关的性质
更换一个可以使用格林公式计算的积分路径与

Q: 设 在单连通区域 内具有一阶连续偏导数, 哪四个命题等价?
A: 1. 内任意光滑封闭曲线 有
2. 内任意光滑曲线 , 曲线积分 ,与路径无关, 只与起点终点有关
3. 在 内存在函数 , 使 ⇐> 为 的全微分
4. 在 内处处有

Q: 设 在复连通区域 内具有一阶连续偏导数, 哪三个命题等价?
A: 1. 内任意光滑封闭曲线 有
2. 内任意光滑曲线 , 曲线积分 ,与路径无关, 只与起点终点有关
3. 在 内存在函数 , 使 ⇐> 为 的全微分

在 内具有一阶连续偏导数

  1. 为单连通:
    处处 为 与路径无关的{充要}条件
  2. 为复连通区域:
    处处 为 与路径无关的{必要不充分}条件

Q: 更换积分路径, 对于新路径有什么要求?
A: 新路径与原来的路径组成的闭区间必须是单连通, 不能是复连通

Q: 什么是单连通区域? 什么是复连通区域?
A: 单连通 (Simply Connected): 区域内部没有洞
复连通 (Multiply Connected): 区域内部有洞

空间曲线

  • 空间第二类曲线积分的计算
    • 参数式
    • 斯托克斯公式

参数式

空间第二类曲线积分的计算
参数式
则有
{}

斯托克斯

空间第二类曲线积分的计算
斯托克斯公式
设 为某空间区域, 为 内的分片光滑有向曲面片, 为逐段光滑的 的边界, 它的方向与 的法向量成{右手系}(左手系 or 右手系), 函数 与 在 内具有{连续的一阶偏导数},
则有斯托克斯公式:

第一类曲面积分形式:
{} 其中 为 的正向单位法向量
第二类曲面积分形式:
{}

如果空间第二类曲线积分的计算可以使用斯托克斯公式
计算结果和 的形状{无关}(有关/无关)

Q: 什么时候使用斯托克斯公式将曲线积分转化为转化为第一类曲面积分, 什么时候转化为第二类曲面积分?
A: 根据曲面 的形状和方程的特点来决定.
选择第一类曲面积分 (参数法), 当曲面 是一个用参数方程描述更方便的几何体时 (如球面、柱面、锥面等), 或者当 (旋度·法向量) 这个点积可以被极大简化时
选择第二类曲面积分 (投影法), 当你能轻松地将曲面 投影到某个坐标平面上, 并且曲面可以被简单地表示为 、 或 的形式.

第二类曲面积分

Q: 如何判断要求的是第一类曲面积分还是第二类曲面积分?
A: 看微元积分的对象
第一类曲面积分对 微元求积分, 形式为
第二类曲面积分对 或者 或者 微元求积分, 形式为

第二类曲面积分特殊的{对称性}

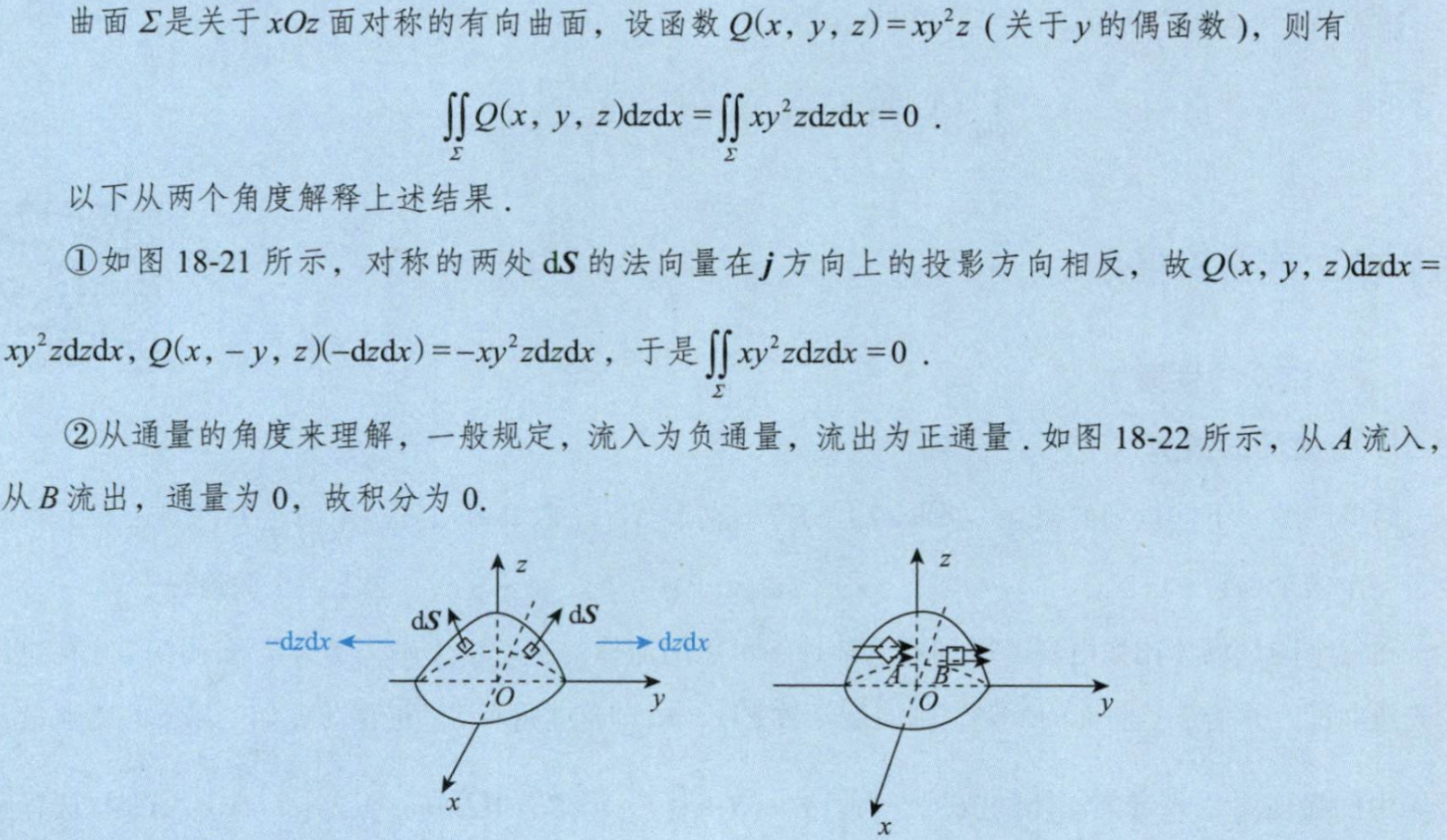
第二类曲面积分的计算
化为二重积分
对于第二类曲面积分

  1. {拆分}
  2. 定方向
  3. {一投二代三计算} 以 为例
    • 将 投影到面 , 计算
    • 将每一个部分化为二重积分计算再求和

Q: 投影方向转化公式
如何将 转化为 ?
A:

第二类曲面积分的计算方法

  1. 投影法 (多用合一投影法)
  2. 极坐标

高斯公式

第二类曲面积分使用高斯公式的三种应用情况

  • 曲面{封闭}并且{没有奇点在内部} 直接使用高斯公式
  • 非封闭曲面, 且{} 可补曲面使其封闭
  • 曲线封闭但有奇点在其内部, 且除奇点外, 其他点都满足{} 换面积分

Q: 空间第二类曲面积分使用高斯公式的三大条件
A: - 围成的是有界闭区域

  • 方向为正向
  • 在 内 有一阶连续偏导

物理应用

Q: 第二类曲面积分的物理意义
A: 有向函数通过某有向曲面的通量

Nabla 算子 或者
与梯度, 散度, 旋度的关系
标量场
向量场
梯度 {c1: }, 为{c1: 向量}场
散度 {c1: }, 为{c1: 标量}场
旋度 {c1: }, 为{c1: 向量}场

方向导数 与梯度 的联系
{} ={}
为 单位化之后的新向量
为梯度与向量 之间的夹角

设有一个空间闭区域 , 其边界是一个分片光滑的封闭曲面 . 如果向量场 在区域 上具有一阶连续偏导数, 那么:

  • 表示在封闭曲面 上的积分, 取外侧为正方向.
  • 是有向面积元.
  • 是场的散度.
  • 是在曲面 所围成的体积 上的三重积分.

核心思想: 高斯公式将一个穿过封闭曲面边界的通量 (Flux)的计算, 转化为了对该边界所围体积内部散度之和的计算.

多元积分总结

第二类曲线积分
平面曲线: 可以考虑使用{格林公式}, 转化为{第一类曲面}
空间曲线: 可以考虑使用{斯托克斯公式}, 转化为{第一类曲面或者第二类曲面}
第二类曲面积分
空间曲面: 可以考虑使用{高斯公式}, 转化为{计算曲面包围的空间体积}

关系图谱