平面, 直线和曲线表达式
平面的五种表达式
- 一般式 {
} - 点法式 {
}, 是一个垂直于平面的法向量 - 三点式 {
} 不共线的三点 - 截距式 {
- 平面束平面束方程:设
与
过
{
直线的四种表达式
- 一般式 {
- 点向式 {
- 参数式 {
- 两点式 {
Q: 直线一般式定义的几何意义
A: 两个面的交线为要表示的直线
Q: 如何将直线一般式方程
转换为平面束方程
A: 引入一个参数
Q: 直线
求直线
A: 直线
使用雅克比行列式求得
空间曲线两种表达式
- 一般式 {
- 参数式 {
Q: 曲线
如何得到
A: 根据
由于在平面
则
Q: 空间曲线一般式的几何背景
A: 两个曲面的交线
空间曲面的四种表达式
- 曲面方程
- 二次曲面各种带有二次项的曲面
- 柱面动直线沿着指定曲线平行移动形成的曲面
- 旋转曲面曲线
混合积
几何意义为
一般用于判断
点到点向式直线的距离
点
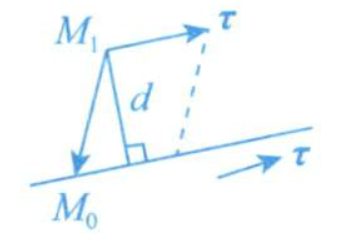
用张成的平行四边形的面积再除以底边
点到一般式平面的距离
点
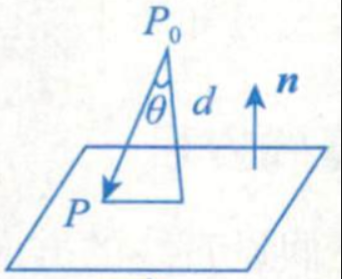
Q: 直线
面为一般表达式
求直线在面上的投影的方程
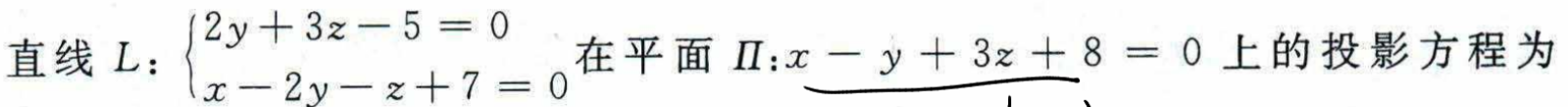
A: 将直线
在平面束方程中找到垂直于
将两个平面方程连立得到投影方程

旋转曲面求解
对于旋转曲面的题目很难说有通解
只能自己寻找几何关系求解
空间曲线
空间曲线参数方程
点
切线向量:
切线方程点向式:{
法平面方程点法式:{
空间曲线一般方程
点
切线向量:
切线方程点向式:{
法平面方程点法式:{
空间曲面
空间曲面隐式方程
法向量:
法线:
切平面方程:
空间曲面显式方程
法向量:
法线:
切平面方程:
空间曲面显式方程
正值法向量{c2: 向上}
负值法向量{c2: 向下}
将空间曲面