极值点,驻点,拐点的判断条件
驻点: {
极值点: {
拐点: {
极值s
极值{不要求}(要求/不要求)
Q: 在点
A: 没有要求
从极值的定义就可以看出
极值点相对于该点附近的其他点而言的
只要比该点的某个邻域内所有点大或小
就可以判断该点是极值
该点有没有连续性不影响是否是极值点
Q: 极值的直观定义
A: 对于函数
Q: 费马定理的定义
A:
一阶可导点为
Q: 为什么一阶可导点为
A:
充分:
例如形如
显然
但
从极值的第三充分条件判断可知
是否是
必要:
直接用费马定理就可以了
从极值点的定义看, 要求
Q: 判断极值的第一充分条件
A: 去心邻域内一阶导数值判断
设
若
若
若
Q: 判断极值的第二充分条件
A: 一阶导数值等于零, 二阶导数值存在
设
若
若
Q: 判断极值的第二充分条件是必要条件吗?
A: 注意是 不必要 条件
可以由第三充分条件证明
例如
当
函数于
在
Q: 判断极值的第三充分条件
A: 第二充要条件的推广
设
当
当
Q: 极值点与驻点,不可导点之间的关系
A: 极值点⊆ 驻点 ∪ 不可导点
驻点
Q: 什么是驻点
A: 一阶导结果为
Q: 什么情况下f(x)的驻点等价于极值点?
A: f(x)处处可导
驻点与不可导点的区别

Q: 凹凸性的定义
- 几何角度
A: 从几何的角度很好理解, 注意从代数的理解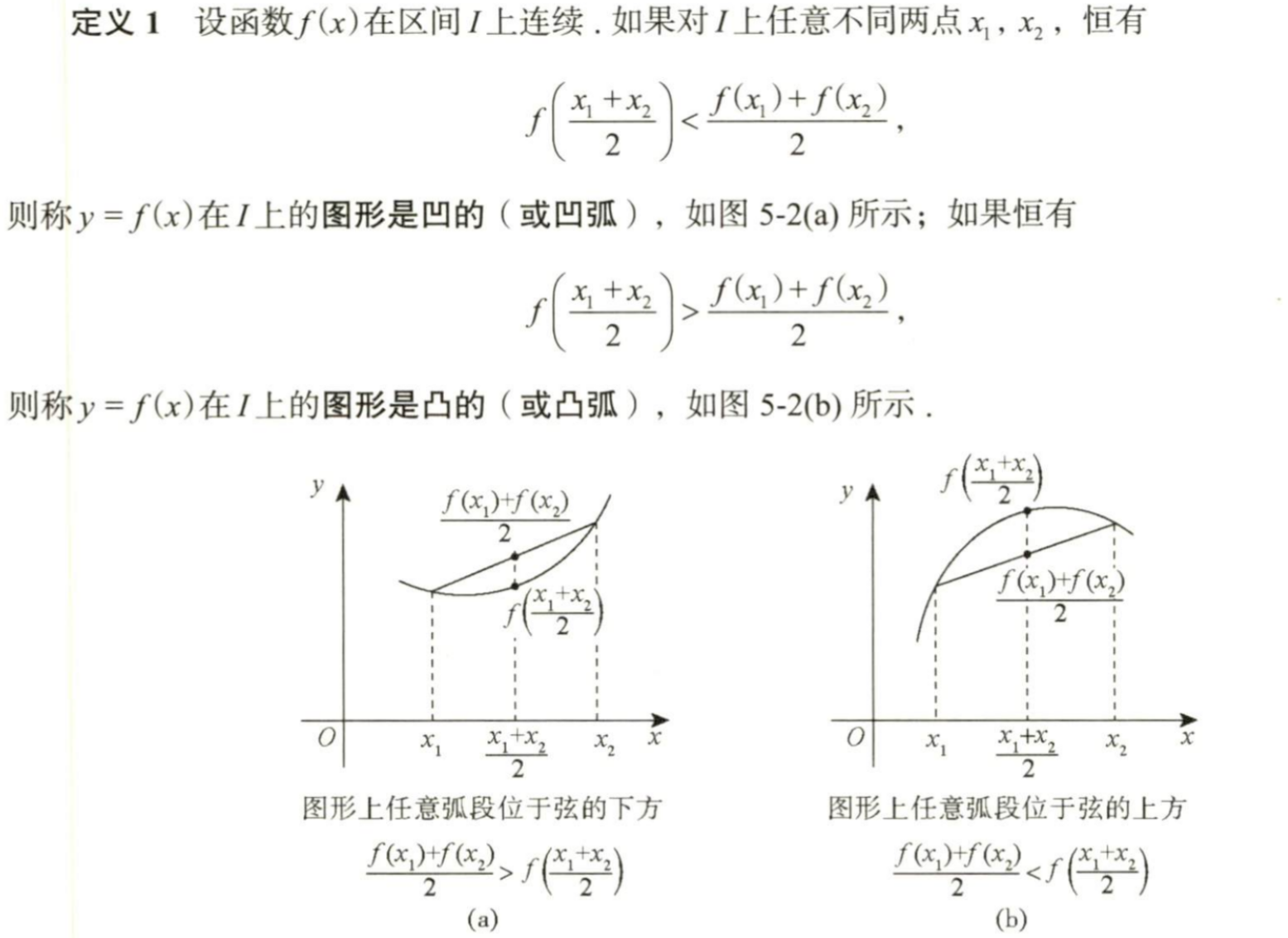
点
某点二阶导为
二阶导为{
例如
Q: 对于
A: 可能
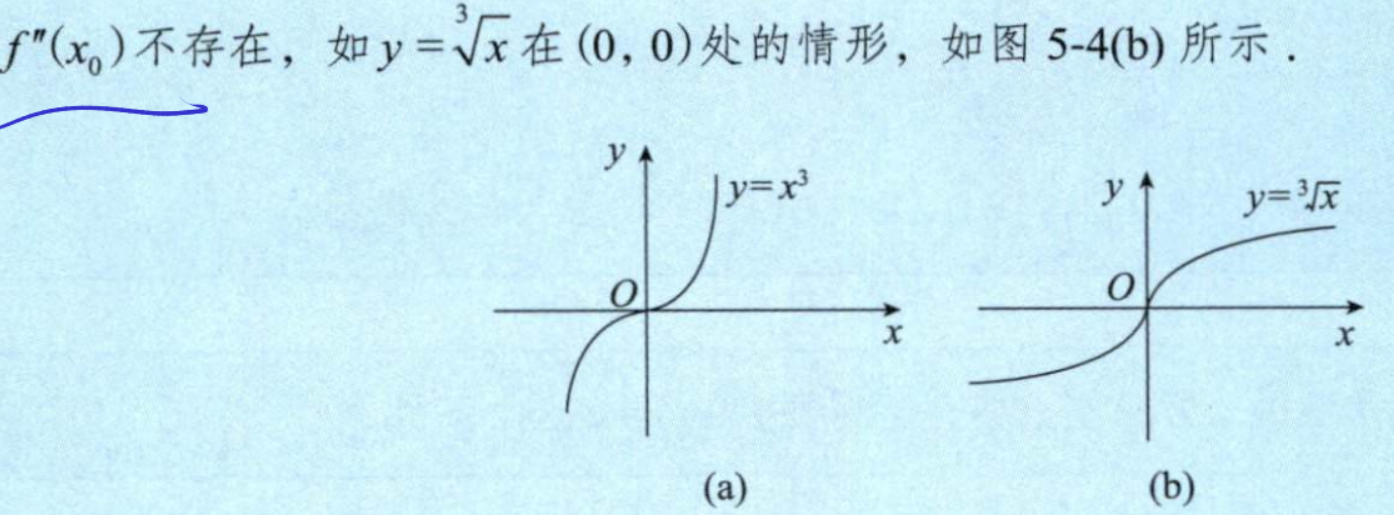
Q: 二阶导不存在仍有可能是拐点吗?
A: 有可能
例如
Q: 通过二阶导判别凹凸性
A: 设函数
若在
若在
Q: 判别拐点的三大充分条件
A: 判断拐点的三大充分条件与判断极值点的三大充分条件相类似

注意第三充分条件不需要
可导点与不可导点
{不可导点}{可以}同时为拐点与极值
不可导点只能从定义出发
极值点的定义是比邻域内的点都要大或者小
拐点的定义是
{可导点}{不可以}同时为拐点与极值点
这点可以从拐点与极值点判断的第三充分条件看出来
多项式极值点与拐点
设多项式函数
记
Q: 设多项式函数
使用穿针引线法,绘制图像的关键口诀
A: 奇穿偶不穿
设多项式函数
强化型穿针引线法
如果
如果
图像判断极值点, 拐点
Q: 已知函数
A: 该点为邻域内最值
Q: 已知函数
A: 该点函数凹凸性改变
Q: 已知函数
A: 该点两边
Q: 已知函数
A: 该点为邻域内最值
Q: 已知函数
A: 可导点:二阶导为0,左右变号
不可导点:左右变号
渐进线
Q: 寻找渐近线的过程
A: 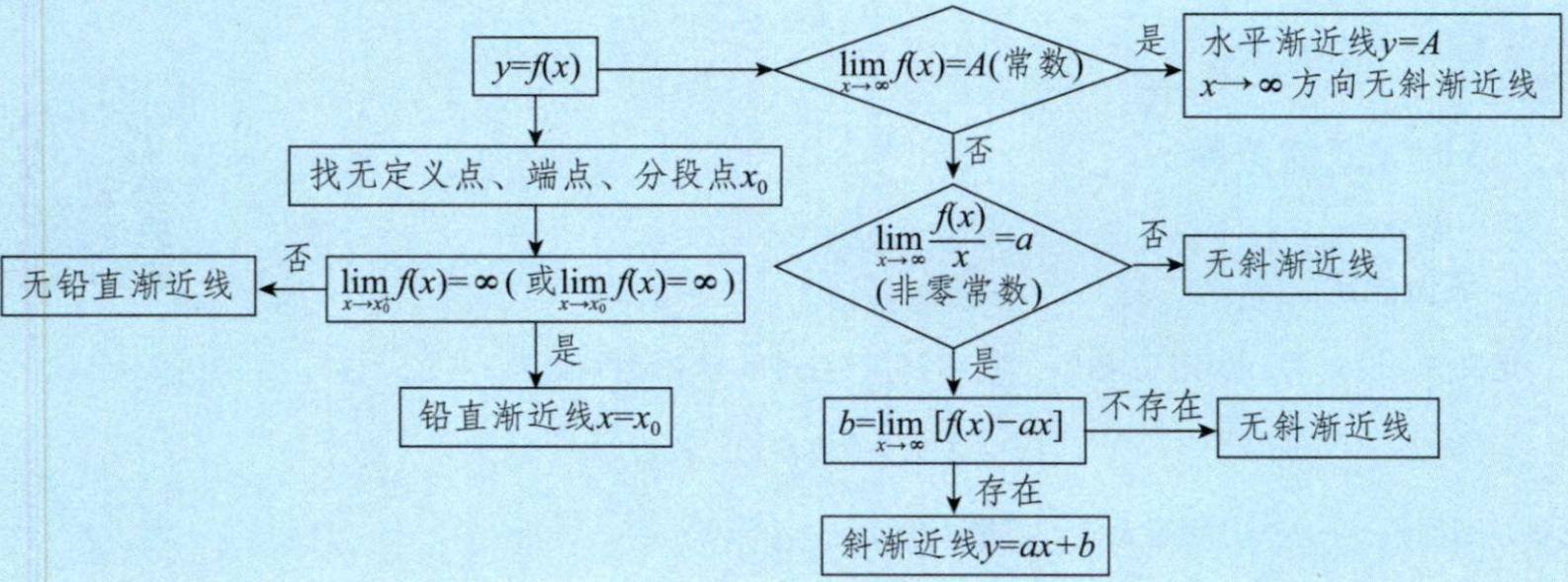
660.20.48
水平渐近线与函数图像{可能有}交点.

Q: 求斜渐近线
A: 斜渐近线一般出在已知极限求参数的题目中
求
求最值
Q: 求
A: 
Q: 求
A: 
曲率
设
{$$
k=\frac{|y^{\prime\prime}|}{[1+(y^{\prime})^{2}]^{\frac{3}{2} } }