矩阵乘法满足{分配率, 结合率}
不满足{交换律, 消去律}
现有矩阵A与列向量alpha
{
转置
转置的性质
Q:
A: 转置矩阵存在秩保持定理
对称矩阵与反对称矩阵的定义设
逆
逆的性质
Q: 一个
存在左逆
存在右逆
A: 左逆
右逆
逆的求法
逆的定义:
初等变换法:
伴随矩阵法:
分块矩阵的逆设
Q: 分块矩阵的秩
现有
什么条件下
A:
或者
秩
在
位于这些行与列的交叉点上的
Q: 秩的原始定义 (子式角度)
A: 最大的非零子式的阶数
Q: 加边法定理描述
A: 矩阵
为充要条件
零矩阵的秩为{零}
若矩阵
若矩阵
满秩的定义
设
若
若
设
设
设
对于一个
{c1:
Q: 对于一个
当
A: 仍然成立
即使是列向量
{c1:
行满秩与列满秩的秩保持定理
若
若
Q: 为什么行满秩与列满秩的秩保持定理成立?
若
若
A: 以
自然
设
秩一矩阵的特殊性质
- 有{c1: n-1}重特征值{c1:0}(仅在
- 唯一非零特征值等于{c1:
伴随
伴随矩阵的形式
设
Q:
A: 不要求
即不论
上标运算的{可交换性}
线性代数是中上标运算可以交换
上标有
对于非零 n 阶矩阵

Q:
A: 相等
初等矩阵
初等矩阵的定义
单位矩阵
三种初等变换对应三种初等变换矩阵:
{两行 (列) 交换} 记作 {
{某行 (列) 乘以非零常数
某行 (列) 乘以非零常数
左乘: {对行操作第
右乘: {对列操作第
初等行变换为{c1: 左乘}(左乘/右乘) 相应的初等变换矩阵
初等列变换为{c1: 右乘}(左乘/右乘) 相应的初等变换矩阵
可逆矩阵的初等分解定理
可逆矩阵可以写成有限个{初等矩阵}的乘积
初等变换矩阵的性质
Q: 初等变换矩阵会改变行列式的值吗?
即
A: 不恒成立
等价
Q: 矩阵
A: 1.
2.
Q: 矩阵
A: 1.
2. 存在
Q: 已知矩阵A与矩阵B
若AP=B.且P可逆,如何计算P?
A: 视作多个Ax=b一起计算
联立,化为行最简型
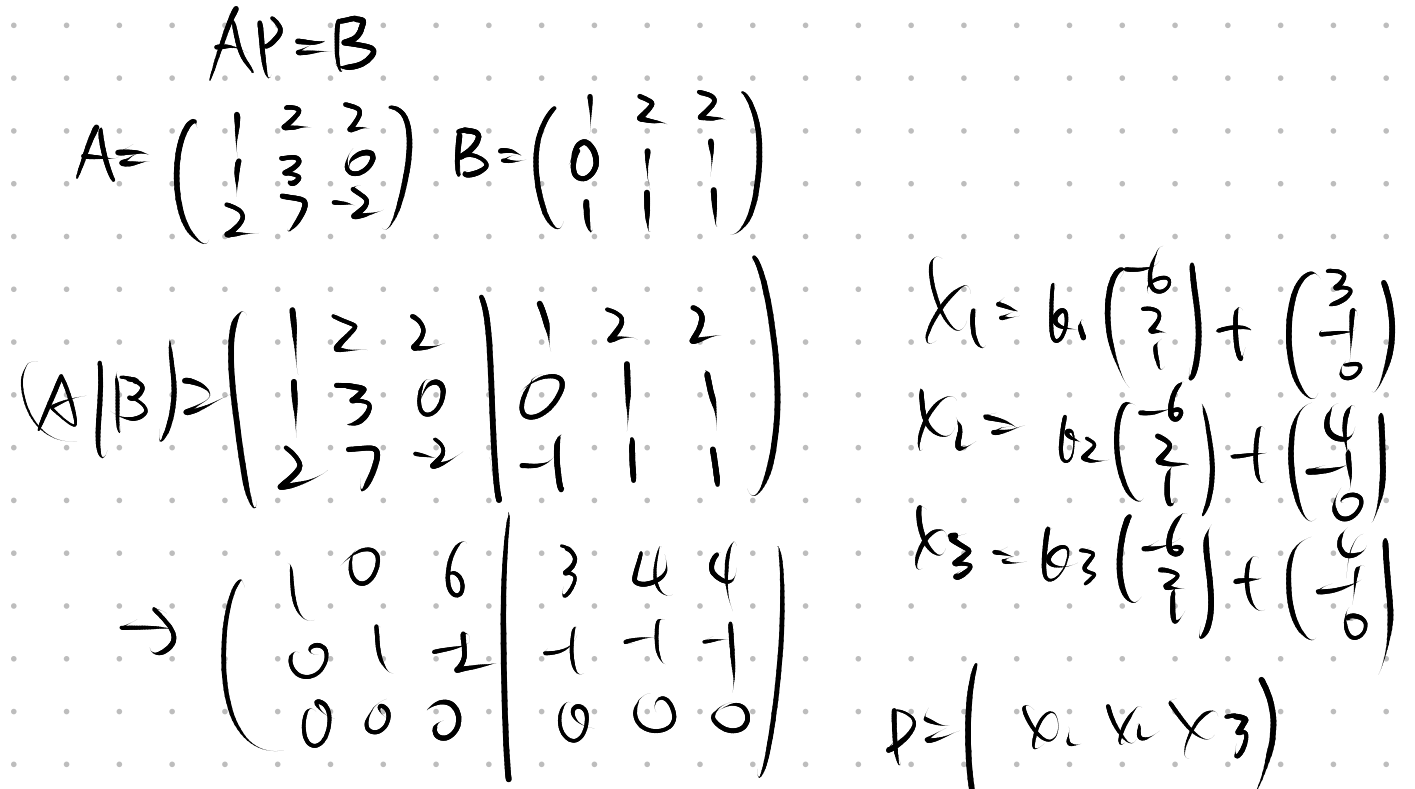
Q: 矩阵
A: 1.
2.
Q: 为什么
A: A, B 为同形矩阵, 并且
对 B 矩阵进行初等行变换与初等列变换, 可以得到 A 矩阵
即
符合矩阵等价的定义,